《高等数学》课程教学资源（PPT课件）第十二章 无穷级数 12-06 第七节 傅里叶（Fourier）级数（series）

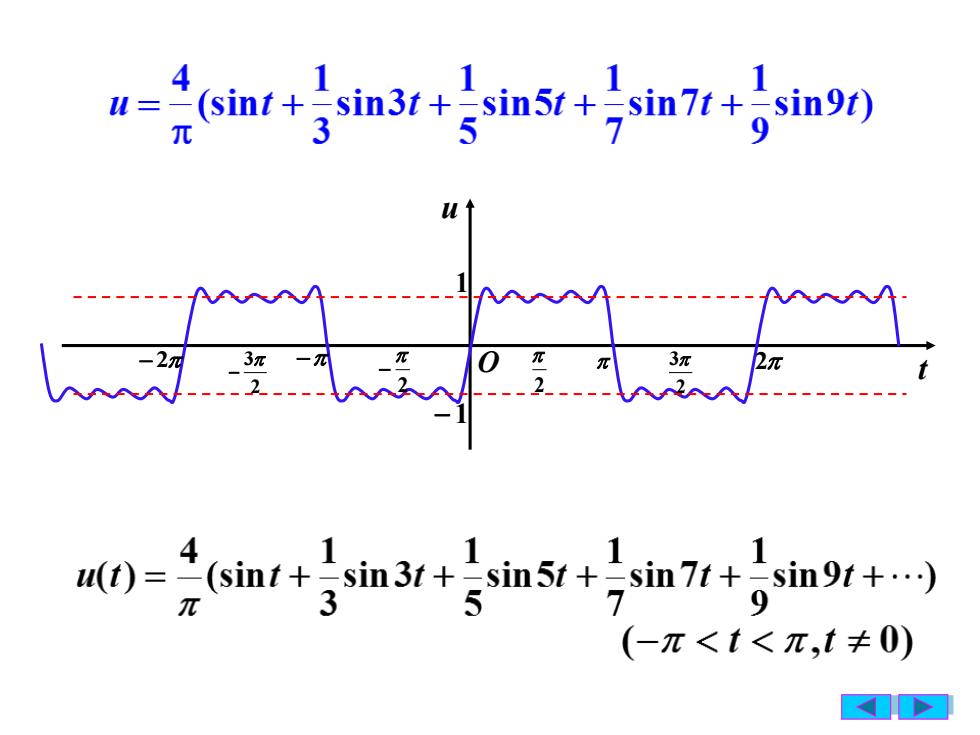
sin5t +sin7t +sin9t)sint +sin3t +U=359元uTsin9t +in3tn5tu(t)=sintnt3元(一元<t<元,t0)

11 O t u 1 − 1 − 2 − 2 2  − 2   2 3 − 2 3

设想一个较复杂的周期运动（如矩形波)分解为简谐振动的迭加·会给分析问题带来方便反映在数学上,是把一个复杂的周期函数(t表示为各类正弦函数A,sin(nのt+@n)的迭加，即A, +ZA, sin(not + pn)谐波分析n=1或再利用三角恒等式，变形为8A, + Z(A, sinn cosnot + A, cosPn sinnot)n=1A

12 设想 一个较复杂的周期运动(如矩形波)分解 为简谐振动的迭加.会给分析问题带来方便. 是把一个复杂的周期函数 f(t) sin( ) n n A nt + 反映在数学上, 表示为各类正弦函数 的迭加,   = + + 1 0 sin( ) n n n A A nt  谐波分析 或再利用三角恒等式,   = + + 1 0 ( sin cos cos sin ) n n n n n A A  nt A  nt 变形为 即

8A + E(A, sin g,cos not + A, cossg,sinnot)n=1今= Ao, a, = A, sinPn, b, = A, cospn, ot = x.2LO三角级数+ E(a, cos nx +b, sinnx)2n-函数f(t)满足什么条件,才能展为三角级数?=1系数ao,an,b,如何确定?为简便计,先来讨论为周期的函数解决上述问题起着关键作用的是：三角函数系的正交性（orthogonality)

13 三角级数   = + + 1 0 ( sin cos cos sin ) n n n n n A A  nt A  nt 函数 f (t) 满足什么条件, 系数 a an bn , , 0 才能展为 如何确定? 为简便计,先来讨论以 为周期的函数 f(x), 2 解决上述问题起着关键作用的是: 三角函数系的正交性(orthogonality).  = 1 三角级数?

orthogonality二、三角函数系的正交性三角函数系1, cosx, sinx, cos2x, sin2x, ...cosnx, sinnx, ...的正交性是指：其中任何两个不同的函数的乘积在一个周期长的区间[一元,元]上的积分为零,而任一个函数的自乘(平方)在[一元,元]上的积分为元或为2元.即有1 .sin nxdx = 0[" 1’dx= 2元1.cosnxdx 元元元A

14 1, 三角函数系 二、三角函数系的正交性 的正交性是指:其中任何两个不同的函数的乘积 在一个周期长的区间 [−, ]上的积分为零， 而任 一个函数的自乘(平方)在 cos x,sin x, cos 2x, sin2x, cosnx, sinnx,  [− , ]上的积分为或 为2 . −   dx − =   dx = 0 即有 1 dx 2 −   = 2 orthogonality

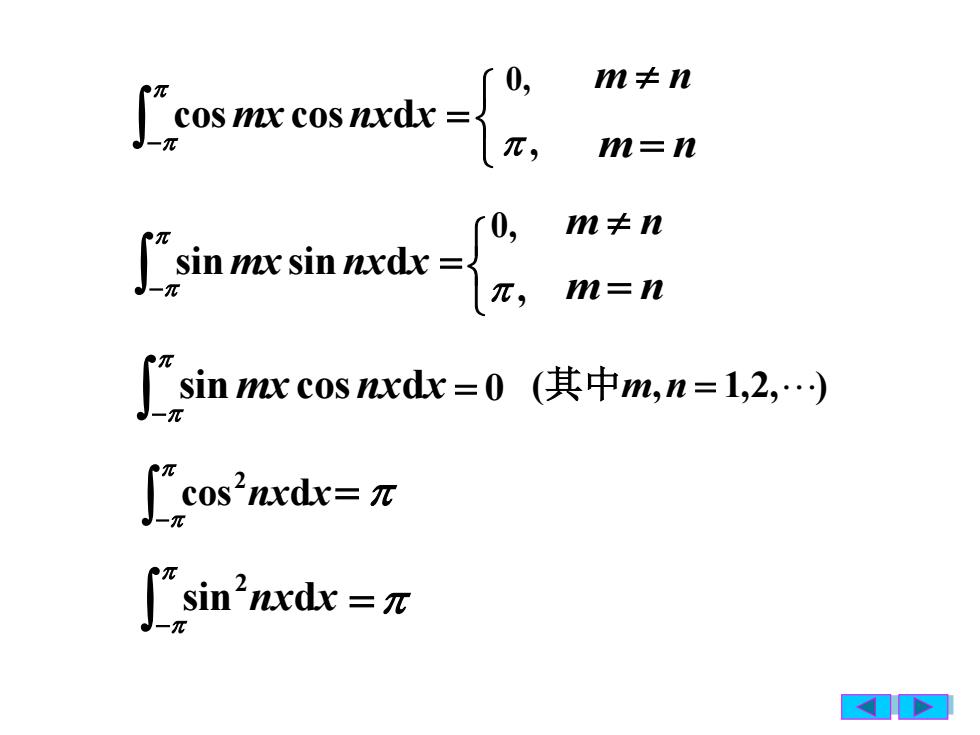
0,m≠ncos mx cos nxdx :元元,m=nr0,m+nsin mx sin nxdx =m=n元元，sinmx cos nxdx = 0 (其中m,n=1,2,...)一元?元cos'nxdx=元元2/Asin°nxdx =元元A

15 = −   sinmx sin nxdx −   sinmx cos nxdx (其中m,n = 1,2, ) cos nxdx 2 −   sin nxdx 2 −   0, m  n  , m = n = 0 =  = = −   cosmx cosnxdx 0, m  n   , m = n     