w=sin(z)实邮的图像 300 200 100 0 -100 -200 -300 10 5 10 0 5 0 5 5 y -10-10

上游充通大学 三角函数的基本性质 SHANGHAI JIAO TONG UNIVERSITY (1)当z∈R,正余弦函数即通常意义下的R上的三角函数。 (2)cosz是偶函数,sinz是奇函数. e-)+e-)ee+e c0s(-z)= cosz, 2 2 (3)cosz和sinz是以2π为周期的周期函数: e(z+2r)-ei+2) sin(z+2π)= =S1n2, 2i
三角函数的基本性质 (3) cosz和sinz是以 为周期的周期函数: sin , 2 sin( 2 ) ( 2 ) ( 2 ) z i e e z i z i z = − + = + π − + π π (2) cosz是偶函数,sinz是奇函数. cos , 2 2 cos( ) ( ) ( ) z e e e e z i z i z iz iz = + = + − = − − − − 2π (1)当 , z R ∈ 正余弦函数即通常意义下的R上的三角函数

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY (4)基本所有三角恒等式仍然成立. (a)sin2 z+cos2 z=1. 因为osg+sn2:-(e+8+e, -12 2 2i e2:+e2:+2e2:+e2:-2 =1. 4 2 (b)sin(z1±z2)=sinz1c0sz2±c0sz1Sinz2, C0s(21±z2)=c0sz1c0sz2干SinZ1Sinz2:
( )sin cos 1. 2 2 a z + z = 1. 2 2 4 2 ) 2 ) ( 2 cos sin ( 2 2 2 2 2 2 2 2 = + − − + + = − + + + = − − − − i z i z i z i z iz iz iz iz e e e e i e e e e 因为 z z (4) 基本所有三角恒等式仍然成立. cos( ) cos cos sin sin . ( )sin( ) sin cos cos sin , 1 2 1 2 1 2 1 2 1 2 1 2 z z z z z z b z z z z z z ± = ± = ±

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY (5)cosz和sinz在整个复平面解析. (cosz)'=-sin z,(sin z)'=cos z. 证明: d d +e i ie ie -iz z e e 二 dz dz 2 2 2i d d i-ei ie+ie 二 CoS Z. dz dz 2i 2i 2
(5) cosz和sinz在整个复平面解析. 证明: (cosz)'= −sin z, (sin z)'= cosz. cos . 2 2 2 sin sin , 2 2 2 cos z e e i ie ie i e e dz d z dz d z i e e ie ie e e dz d z dz d iz iz iz iz iz iz iz iz iz iz iz iz = + = + = − = = − − = − − = + = − − − − − −

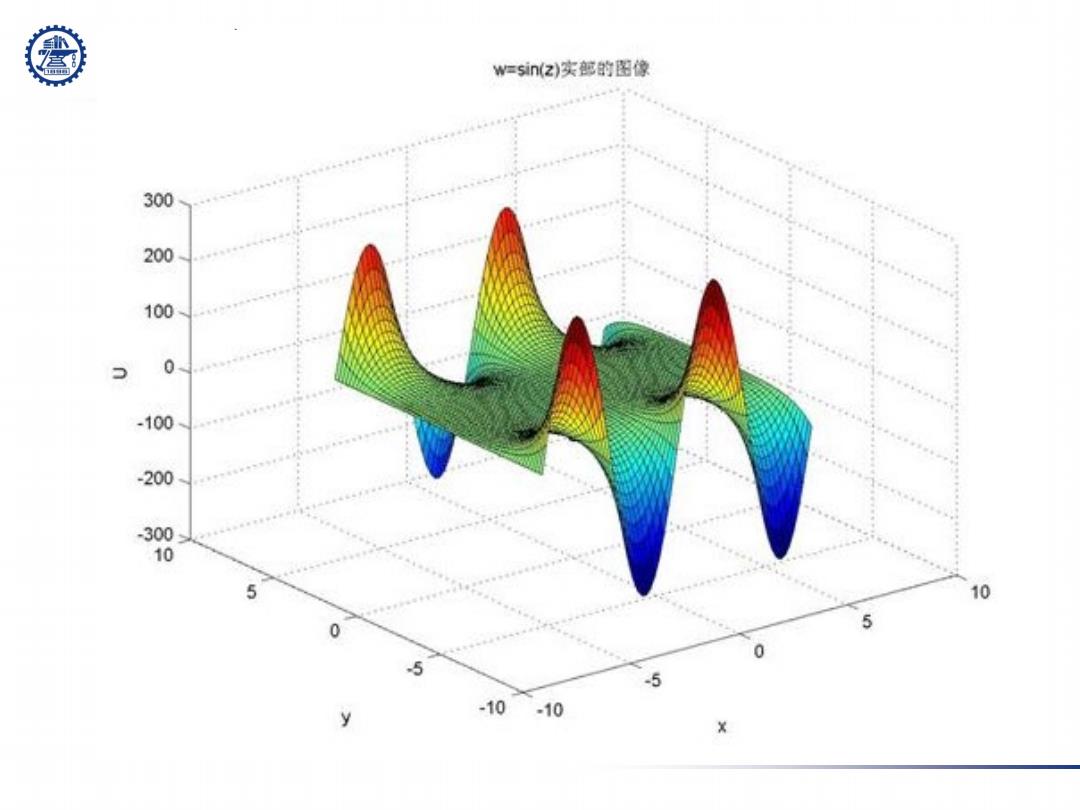
上游充大粤 SHANGHAI JIAO TONG UNIVERSITY (6) cosz在复平面的零点是 π Z= +kπ(k∈Z). 2 sinz在复平面的零点是 z=kπ(k∈Z). (7)|cosz,Isinz在复域上不再有界
(6) cosz在复平面的零点是 sinz在复平面的零点是 ( ). 2 z = + kπ k ∈ Z π z = kπ (k ∈ Z). (7) | cos |,| sin | z z 在复域上不再有界