《高等数学》课程教学资源（课件讲稿）第四章_4.1

(?)= xsx'dx.例1 求.6x+解x:661求例2 dx.1 + x2解：(arctan2--1dx = arctan x + C.高等数学（上册）

例1 求 5 x dx.  解 , 6 5 6 x x          6 5 6 d . x  x x   C  解 例2 求 2 1 1 dx.  x    , 1 1 arctan 2 x x     2 1 1 dx arctan x C. x     

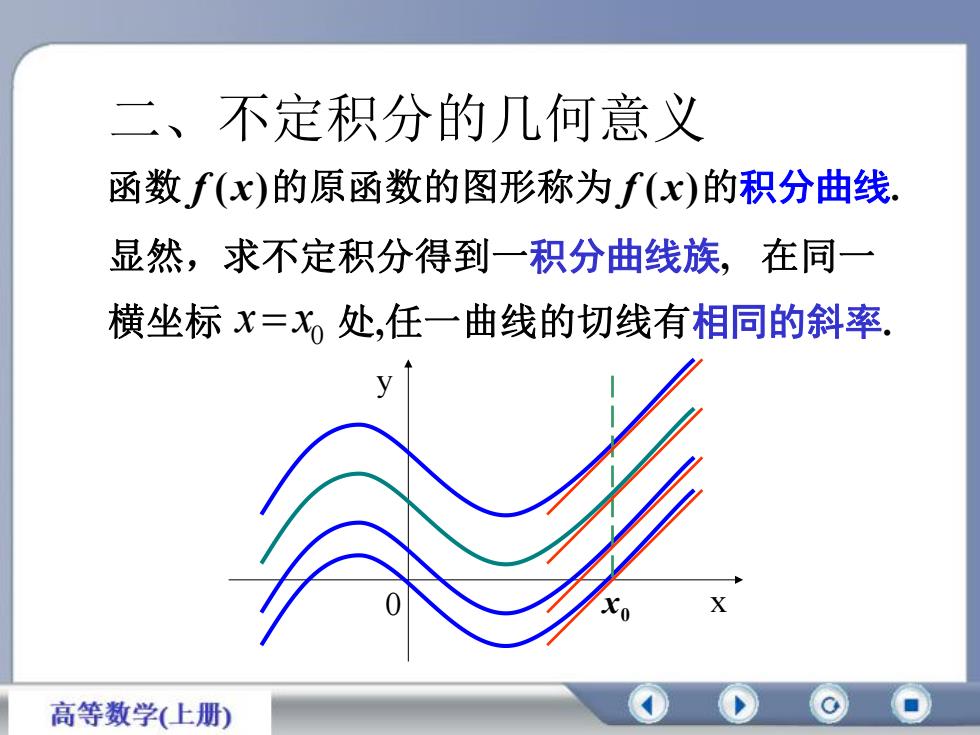
不定积分的几何意义二函数f(x)的原函数的图形称为f(x)的积分曲线在同一显然，求不定积分得到一积分曲线族横坐标x=处,任一曲线的切线有相同的斜率V0Xx0高等数学（上册）

二、不定积分的几何意义 函数 f (x)的原函数的图形称为 f (x)的积分曲线. 显然，求不定积分得到一积分曲线族, 横坐标 处,任一曲线的切线有相同的斜率. 0 xx 0 x y 0 x 在同一

基本积分表（教材198页）一ru+1xu+1实例ru+C=dxμ+1+(u ± -1)启示能否根据求导公式得出积分公式？结论既然积分运算和微分运算是互逆的，因此可以根据求导公式得出积分公式高等数学（上册）

实例    x x           1 1 1 1 d . x x x C          启示 能否根据求导公式得出积分公式？ 结论 既然积分运算和微分运算是互逆的， 因此可以根据求导公式得出积分公式. (  1) 三、 基本积分表（教材198页）