
苏本堂 ao =-["f(x)dx ∫,fax)coskxdx=_coskxdx+- 2J-π a.costienmdr+6jomtanxdr 00 + =acos2kxdx=aπ 。π (利用正交性) &-号./()eoskxdx(t=1,2-) 类似地,用sin kx乘①式两边,再逐项积分可得 sinkrdx (
山东农业大学 高等数学 主讲人:苏本堂 = + − − kx x a f x kx x cos d 2 ( ) cos d 0 = + n 1 + − a kx nx x n cos cos d b kx nx x n cos sin d − a kx x k cos d 2 − = a f x kx x k ( ) cos d 1 − = ( k =1, 2, ) (利用正交性) ( )sin d ( 1, 2, ) 1 = = − b f x kx x k k a f (x)d x 1 0 − = 类似地, 用 sin k x 乘 ① 式两边, 再逐项积分可得

fN-受+2(a,asn+asn) 00 n=l a,-i/0 wmdx @=r0.l) 0。上)simdx (a=1.2, ② 由公式②确定的an,bn称为函数 ∫(x)的傅里叶系数;以f(x)的傅里 叶系数为系数的三角级数①称为 ∫(x)的傅里叶级数
山东农业大学 高等数学 主讲人:苏本堂 叶系数为系数的三角级数 ① 称为 的傅里叶系数 ; ( ) = = + + 1 0 cos sin 2 ( ) n n n a nx b nx a f x − = = ( ) cos d ( 0,1, ) 1 an f x n x x n 由公式 ② 确定的 ① ② 以 − = = ( )sin d ( 1, 2, ) 1 bn f x n x x n 的傅里 的傅里叶级数 . 称为函数

主 苏本堂 定理3(收敛定理,展开定理) 设f(x)是周期为2π的 周期函数,并满足狄利克雷(Dirichlet)条件: 1)在一个周期内连续或只有有限个第一类间断点, 2)在一个周期内只有有限个极值点, 则f(x)的傅里叶级数收敛,且有 注意:函数展成 傅里叶级数的条 9+∑(a,cosr+b,sinr) 件比展成幂级数 2 n=1 的条件低得多 f(x), x为连续点 +、x为间断局 2 其中an,bn为f(x)的傅里叶系数.(证明略)
山东农业大学 高等数学 主讲人:苏本堂 定理3 (收敛定理, 展开定理) 设 f (x) 是周期为2的 周期函数, 并满足狄利克雷( Dirichlet )条件: 1) 在一个周期内连续或只有有限个第一类间断点; 2) 在一个周期内只有有限个极值点, 则 f (x) 的傅里叶级数收敛, 且有 = f (x) , , 2 ( ) ( ) + − f x + f x x 为间断点 其中 n n a , b 为 f (x) 的傅里叶系数 . ( 证明略 ) x 为连续点 注意: 函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多

例1.设f(x)是周期为2元的周期函数,它在[-π,π) 上的表达式为 -π≤x<0 0≤x<π 将f(x)展成傅里叶级数 解:先求傅里叶系数 a,-∫f0 cox =0 (n=0,1,2,.)
山东农业大学 高等数学 主讲人:苏本堂 例1. 设 f (x) 是周期为 2 的周期函数 , 它在 上的表达式为 − − = x x f x 1, 0 1, 0 ( ) 解: 先求傅里叶系数 = − + − 0 0 1 cos d 1 ( 1) cos d 1 nx x nx x = 0 ( n = 0 ,1, 2 , ) 将 f (x) 展成傅里叶级数. o y x −1 − 1
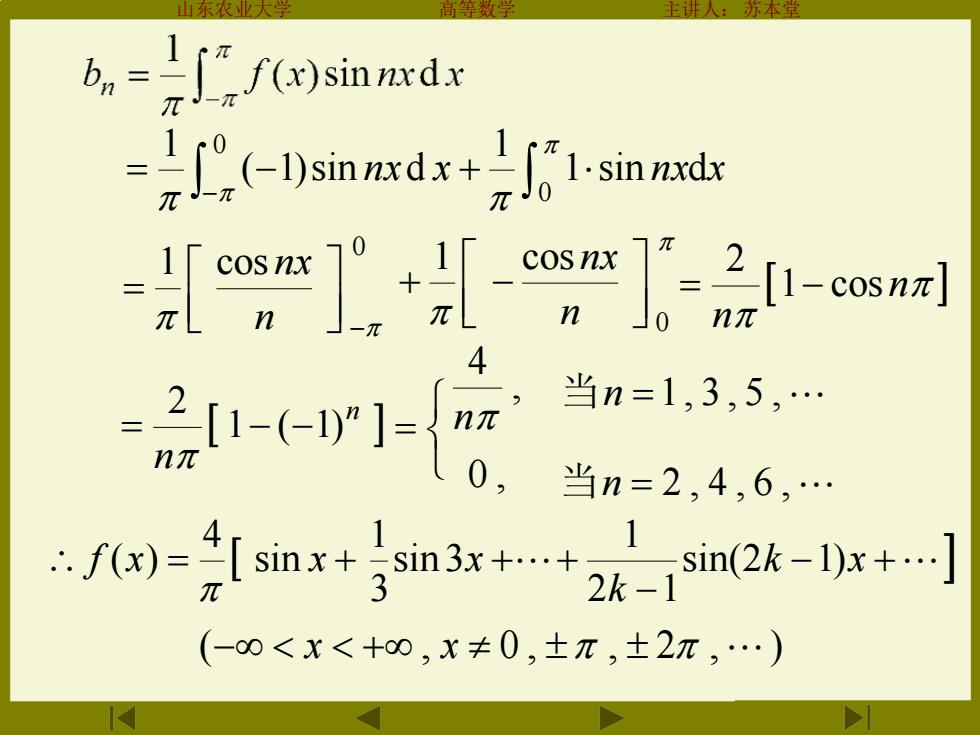
方本 b,=∫f)sind (-sin tdxsin m],"]-w w1 4 当n=1,3,5,. 当n=2,4,6,. 2k- sin(2k-l)x+.] (-00<x<+0,x≠0,士π,±2π,.)
山东农业大学 高等数学 主讲人:苏本堂 = − + − 0 0 1 sin d 1 ( 1)sin d 1 nx x nx x 0 1 cos − = n nx 0 1 cos − + n nx n n 1 cos 2 = − n n 1 ( 1) 2 = − − = , 4 n 0 , 当n =1, 3 , 5 , 当n = 2 , 4 , 6 , f x = sin x + 4 ( ) sin 3x + 3 1 − + − + k x k sin(2 1) 2 1 1 (− x + , x 0 , , 2 , )