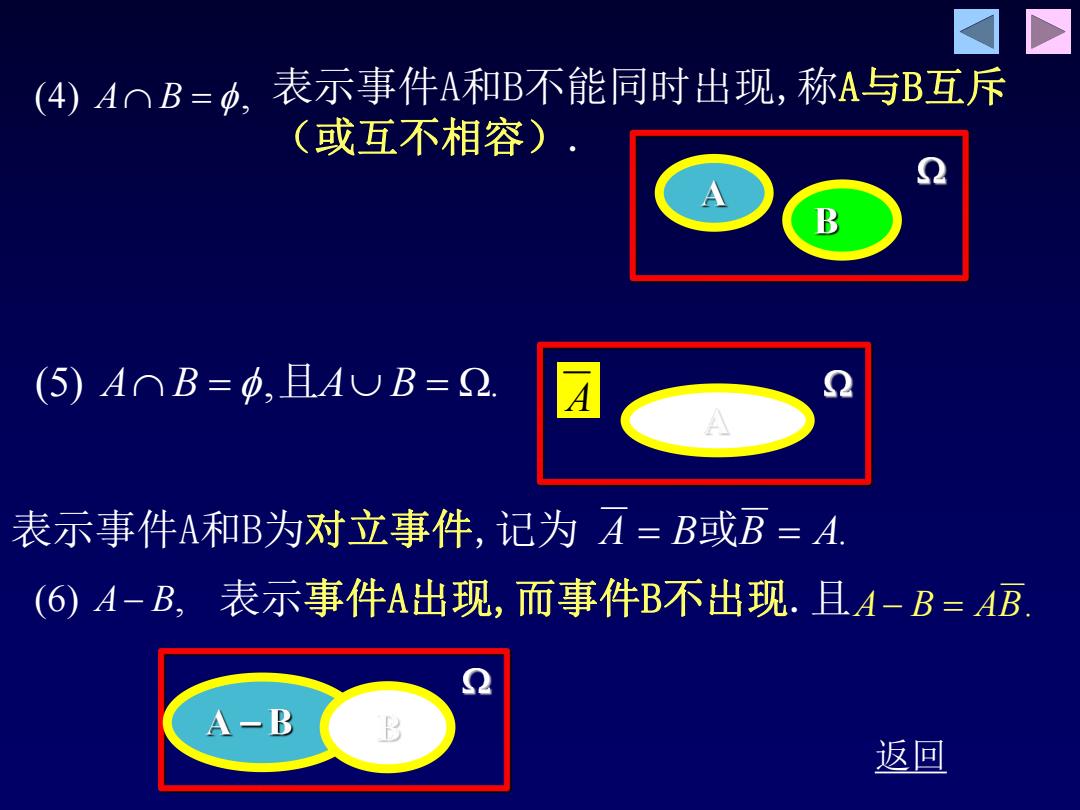
(4)AnB=, 表示事件A和B不能同时出现,称A与B互斥 (或互不相容) A B (5)A⌒B=中,且AUB=2 表示事件A和B为对立事件,记为A=B或B=A. (6)A-B,表示事件A出现,而事件B不出现.且A-B=AB A-B 返回
返回 (5) A B ,且A B . 表示事件A和B为对立事件,记为 A B或B A. A (4) A B , 表示事件A和B不能同时出现,称A与B互斥 (或互不相容). (6) A B, 表示事件A出现,而事件B不出现.且A B AB

同集合有结合律、分配律、交换律、对偶律 (AUB)UUC=AU(BUC),(A⌒B)⌒C=A∩(B∩C); (AUB)∩C=(A∩C)(BOC),(A⌒B)UC=(AUC)∩(BUC) AUB=BUA,A∩B=B∩A AUB=A0B, 表示事件A和事件B都不出现. A⌒B=AUB,表示事件A和事件B至少有一个不出现. 注以上f米可推广为94=合不,口4=9A i=1 返回
返回 A B A B, 表示事件A和事件B都不出现. A B A B, 表示事件A和事件B至少有一个不出现. 注 以上结果可推广为 i n i i n i i n i i n i A A A A 1 1 1 1 , 同集合有结合律、分配律、交换律、对偶律 , ; ( ) ( ) ( ),( ) ( ) ( ); ( ) ( ),( ) ( ); A B B A A B B A A B C A C B C A B C A C B C A B C A B C A B C A B C

课堂练习 .设事件A={甲种产品畅销,乙种产品滞销}, 则A的对立事件为(④ ①甲种产品滞销,乙种产品畅销: ②甲、乙两种产品均畅销; ③甲种产品滞销: ④甲种产品滞销或者乙种产品畅销。 2.设x表示一个沿数轴做随机运动的质点位 置,试说明下列各对事件间的关系 ①A={x-a<o},B={x-a<o}(o>0) ②A={x>20},B={x≤20} A与B对立 ③A={x>22},B={x<19} A与B互斥 返回
返回 1.设事件A={甲种产品畅销,乙种产品滞销}, 则A的对立事件为( ) ①甲种产品滞销,乙种产品畅销; ②甲、乙两种产品均畅销; ③甲种产品滞销; ④甲种产品滞销或者乙种产品畅销。 课堂练习 ④ A B A与B对立 A与B互斥 2.设x表示一个沿数轴做随机运动的质点位 置,试说明下列各对事件间的关系 ①A={|x-a|<σ},B={x-a<σ}(σ>0) ②A={x>20},B={x≤20} ③A={x>22},B={x<19}

例1设A、B、C为任意三个事件,试用它们表示下列事件 (1)A、B出现,C不出现; (2)A、B、C中恰有一个出现; (3)A、B、C中至多有一个出现: (4)A、B、C中至少有一个出现 解 (1)ABC=AB-C=AB-ABC.(2)ABC+ABC+ABC (3)ABC+ABC+ABC+ABC (4)ABC=A+B+C 例2设A、B、C为任意三个事件,证AB+AB+AB=AB 证左=AB+AB+AB+AB=(AB+AB)+(AB+AB) =A(B+B)+(A+A)B=A+B=AB= 返回
返回 例1 设A、B、C为任意三个事件,试用它们表示下列事件: (1) A、B出现,C不出现; (2) A、B、C中恰有一个出现; (3) A、B、C中至多有一个出现; (4) A、B、C中至少有一个出现. 解 (1) ABC AB C AB ABC. (2) ABC ABC ABC (3) ABC ABC ABC ABC (4) ABC A B C 例2 设A、B、C为任意三个事件,证 AB AB AB AB 右 左 A B B A A B A B AB AB AB AB AB AB AB AB AB ( ) ( ) 证 ( ) ( )

第1.1节 随机事件及其运算 概率论与数理统计的研究对象 概率论与数理统计是研究随机现象统计 规律性的一门科学。随机现象的普遍存在性 决定了它的广泛应用性。 返回
返回 概率论与数理统计的研究对象 概率论与数理统计是研究随机现象统计 规律性的一门科学。随机现象的普遍存在性 决定了它的广泛应用性。 第1.1节 随机事件及其运算