
Integer Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University 4口48+4三4至,至)只0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 1/42
Integer Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 1 / 42

Introduction Introduction The Branch-and-Bound Method Implicit Enumeration The Cutting Plane Algorithm 4口,4得+4艺至,三风0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 2/42
Introduction 1 Introduction 2 The Branch-and-Bound Method 3 Implicit Enumeration 4 The Cutting Plane Algorithm Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 2 / 42

Introduction Definition 1.1 An integer programming problem (IP)is an LP in which some or all of the variables are required to be non-negative integers,i.e.,the Divisibility Assumption in LP does not hold. A pure integer programming problem max3x为+2x2 s.t.x1+9≤6灯,x2≥0,灯,2 integer. A mixed integer programming problem max3x灯+2x2 s.t.+x2≤6,为,x2≥0,x1 integer.. A 0-1 integer programming problem max X1 -X2 s.t. x1+2x2≤2,2x灯-2≤1 ,X9=0or1. Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 3/42
Introduction Definition 1.1 An integer programming problem (IP) is an LP in which some or all of the variables are required to be non-negative integers, i.e., the Divisibility Assumption in LP does not hold. A pure integer programming problem max 3x1 + 2x2 s.t. x1 + x2 ≤ 6 x1, x2 ≥ 0, x1, x2 integer. A mixed integer programming problem max 3x1 + 2x2 s.t. x1 + x2 ≤ 6, x1, x2 ≥ 0, x1 integer. A 0-1 integer programming problem max x1 − x2 s.t. x1 + 2x2 ≤ 2, 2x1 − x2 ≤ 1, x1, x2 = 0 or 1. Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 3 / 42
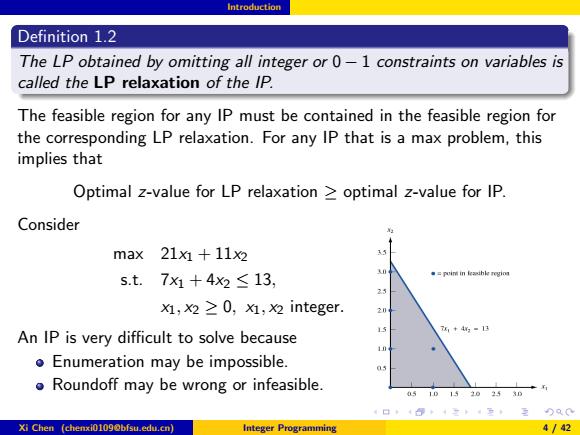
Introduction Definition 1.2 The LP obtained by omitting all integer or 0-1 constraints on variables is called the LP relaxation of the IP. The feasible region for any IP must be contained in the feasible region for the corresponding LP relaxation.For any IP that is a max problem,this implies that Optimal z-value for LP relaxation optimal z-value for IP. Consider max21x为+119 33 s.t.7x+4x2≤13, 灯,x2≥0,灯,2 integer. 7+413 An IP is very difficult to solve because 1 o Enumeration may be impossible. Roundoff may be wrong or infeasible. 05 1D15.20253D )Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 4/42
Introduction Definition 1.2 The LP obtained by omitting all integer or 0 − 1 constraints on variables is called the LP relaxation of the IP. The feasible region for any IP must be contained in the feasible region for the corresponding LP relaxation. For any IP that is a max problem, this implies that Optimal z-value for LP relaxation ≥ optimal z-value for IP. Consider max 21x1 + 11x2 s.t. 7x1 + 4x2 ≤ 13, x1, x2 ≥ 0, x1, x2 integer. An IP is very difficult to solve because Enumeration may be impossible. Roundoff may be wrong or infeasible. Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 4 / 42
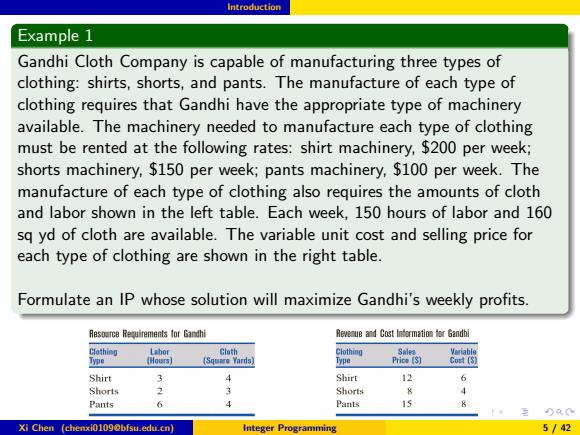
Introduction Example 1 Gandhi Cloth Company is capable of manufacturing three types of clothing:shirts,shorts,and pants.The manufacture of each type of clothing requires that Gandhi have the appropriate type of machinery available.The machinery needed to manufacture each type of clothing must be rented at the following rates:shirt machinery,$200 per week; shorts machinery,$150 per week;pants machinery,$100 per week.The manufacture of each type of clothing also requires the amounts of cloth and labor shown in the left table.Each week,150 hours of labor and 160 sq yd of cloth are available.The variable unit cost and selling price for each type of clothing are shown in the right table. Formulate an IP whose solution will maximize Gandhi's weekly profits. Resource Reguirements lor Gandhi Reveue ad Costtrmatioor Gandhi Clothing Labor Cloth Clothing Salea Variable Hours】 (Square Yards) Type Price (S] Co时(S) Shirt 4 Shirt 12 6 Shorts 2 Shorts Pants 6 Pants 15 )Q0 Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 5/42
Introduction Example 1 Gandhi Cloth Company is capable of manufacturing three types of clothing: shirts, shorts, and pants. The manufacture of each type of clothing requires that Gandhi have the appropriate type of machinery available. The machinery needed to manufacture each type of clothing must be rented at the following rates: shirt machinery, $200 per week; shorts machinery, $150 per week; pants machinery, $100 per week. The manufacture of each type of clothing also requires the amounts of cloth and labor shown in the left table. Each week, 150 hours of labor and 160 sq yd of cloth are available. The variable unit cost and selling price for each type of clothing are shown in the right table. Formulate an IP whose solution will maximize Gandhi’s weekly profits. Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 5 / 42