
简单曲线的复数表示 例1用复数表示复平面上两点z1、z2之间的距离d 冬例2用复数表示复平面上以z为圆心,r为半径的 圆方程 例3用复数表示复平面上以z1、z2为焦点,为长 轴的椭圆方程 ÷例4用复数表示复平面上以z1、z2为焦点,2为 实轴的双曲线方程 冬例5用复数表示复平面上以zn为焦点,x=x为准 线的抛物线方程 lexu@mail.xidian.edu.cn 矩阵论 11
lexu@mail.xidian.edu.cn 矩 阵 论 11 简单曲线的复数表示 例1 用复数表示复平面上两点z1 、 z2之间的距离d 例2 用复数表示复平面上以z0为圆心,r为半径的 圆方程 例3 用复数表示复平面上以z1 、 z2 为焦点,a为长 轴的椭圆方程 例4 用复数表示复平面上以z1 、 z2 为焦点,2a为 实轴的双曲线方程 例5 用复数表示复平面上以z0 为焦点,x= x0为准 线的抛物线方程
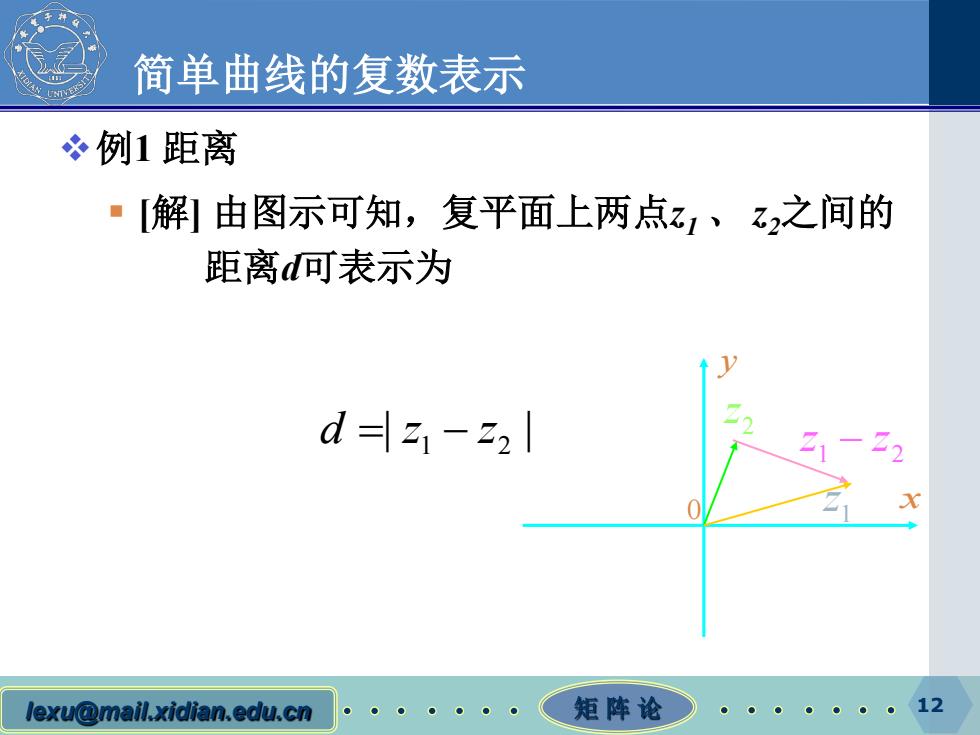
简单曲线的复数表示 冬例1距离 ·[解1由图示可知,复平面上两点z1、2之间的 距离可表示为 d 2-22 lexu@mail.xidian.edu.cn ●● 矩阵论 12
lexu@mail.xidian.edu.cn 矩 阵 论 12 简单曲线的复数表示 例1 距离 [解] 由图示可知,复平面上两点z1 、 z2之间的 距离d可表示为 1 2 z − z y x 0 2 z 1z 1 2 dzz = − | |

简单曲线的复数表示 冬例2圆 ·[解]圆:到定点的距离为常数的点的集合 Z-Z0=r lexu@mail.xidian.edu.cn 矩阵论 °。。。。13
lexu@mail.xidian.edu.cn 矩 阵 论 13 简单曲线的复数表示 例2 圆 [解] 圆:到定点的距离为常数的点的集合 y x 0 0 z z 0 | | zz r − =

简单曲线的复数表示 冬例3椭圆 ■[解]椭圆:到两点的距离之和为常数 |z-21|+|z-22=2a 例4双曲线 ·[解]双曲线:到两点的距离之差为常数 |z-z1|-|z-z2=±2a 例5抛物线 ·[解]抛物线:到定点与定直线的距离相等 lexu@mail.xidian.edu.cn 2-20=X-x
lexu@mail.xidian.edu.cn 矩 阵 论 14 简单曲线的复数表示 例3 椭圆 [解] 椭圆:到两点的距离之和为常数 例4 双曲线 [解] 双曲线:到两点的距离之差为常数 例5 抛物线 [解] 抛物线:到定点与定直线的距离相等 1 2 | | | |2 zz zz a − +− = 1 2 | || | 2 zz zz a − − − =± 0 | | l zz xx − =−