《线性代数》课程教学课件（PPT讲稿，C）初等矩阵

12 1 23 E(2,3)A= 2 2 1 = 3 4 3 3 43 22 1 123 100 1 AE,(2,3)= 221 00 = 2 343010 上页

1 0 0 0 0 1 0 1 0                     2 2 1 3 1 4 3 2 3     =       3 4 1 1 3 2 2 2 3 3 E A (2,3) = 3 AE (2,3) =           3 1 4 1 3 3 2 2 2 1 0 0 0 0 1 0 1 0               =       1 2 1 2 4 3 3 3 2

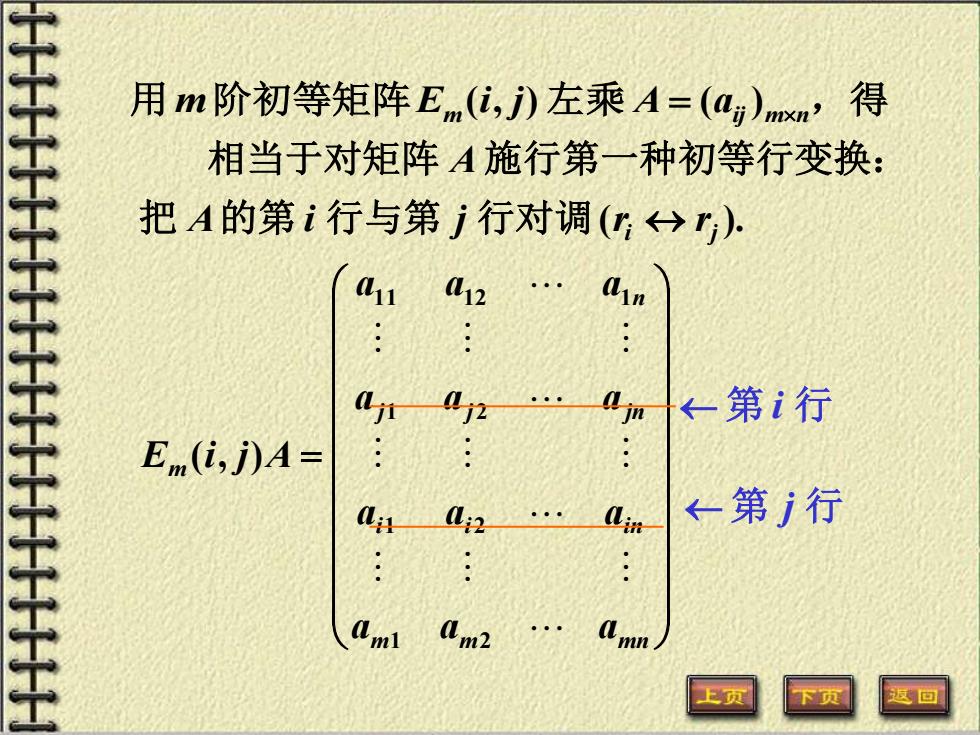
用m阶初等矩阵Em(i,j)左乘A=(a,)mxn,得 相当于对矩阵A施行第一种初等行变换： 把A的第i行与第j行对调(：)r) 11 12 n : ←-第i行 Em(i,j)A= 2 L ←第j行 :: ·· mn 回

用m 阶初等矩阵Em (i, j) 左乘 A = (aij)mn，得                       = m m mn i i in j j jn n m a a a a a a a a a a a a E i j A              1 2 1 2 1 2 1 1 1 2 1 ( , )  第 i 行  第 j 行 ( ). i j A i j r r A 把 的第 行与第 行对调  相当于对矩阵 施行第一种初等行变换：

类似地， 以n阶初等矩阵E,n(i,j)右乘矩阵A, 相当于对矩阵A施行第一种初等列变换： 把A的第i列与第j列对调(c,c), L11 AE,(i,j)= 21 Azn mj

以 阶初等矩阵 右乘矩阵 ， 类似地， n En (i, j) A               = m mj mi mn j i n j i n n a a a a a a a a a a a a AE i j              1 2 1 2 2 2 1 1 1 1 1 ( , ) ( ). i j A i j c c A 把 的第 列与第 列对调  相当于对矩阵 施行第一种初等列变换：

2、1 以数k≠0乘某行或某列 以数k≠0乘单位矩阵的第行(r×k),得初等 矩阵E(i(k). E(i())= ←第i行 回

2、以数 k  0 乘某行或某列 ( ( )). 0 ( ) E i k k i ri k 矩阵 以数  乘单位矩阵的第 行  ，得初等                       = 1 1 1 1 ( ( ))   E i k k  第 i 行

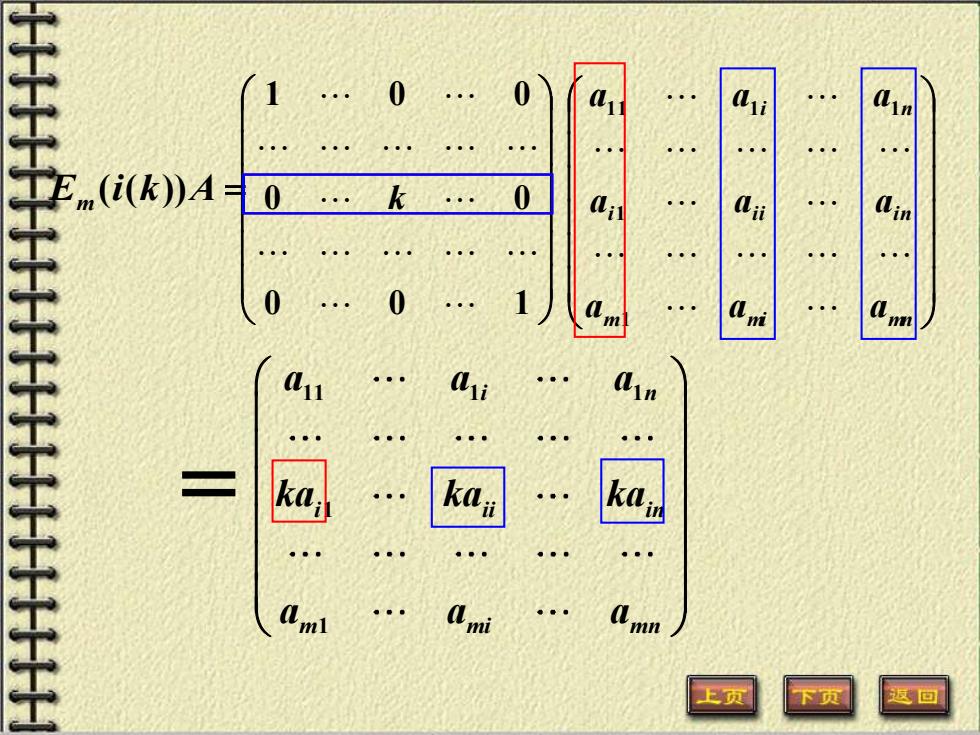
0 0 (i(K))A= 0 0 。 0 mi 1 mi

11 1 1 1 1 i n i ii in m mi mn a a a ka ka ka a a a               ( ( )) E i k A m =                 0 0 1 0 0 1 0 0                 k                 m mi mn i i i i n i n a a a a a a a a a                 1 1 11 1 1 =