
导航 2.做一做:若单位向量a,b,c两两夹角都是60°,且p=a+b-2c, q=2b-a,则pq= 解析pq=(a+b-2c)(2b-a) =2ab+2b2-4bc-a2-ab+2ac -2*242 22 =1+2-21+1 1 答案号
导航 2.做一做:若单位向量a,b,c两两夹角都是60° ,且p=a+b-2c, q=2b-a,则p·q= . 解析:p·q=(a+b-2c)·(2b-a) =2a·b+2b2 -4b·c-a 2 -a·b+2a·c =2×𝟏 𝟐 +2-4×𝟏 𝟐 -1- 𝟏 𝟐 +2×𝟏 𝟐 =1+2-2-1- 𝟏 𝟐 +1 = 𝟏 𝟐 . 答案: 𝟏 𝟐

导航 四、向量的坐标运算 1.填空:己知a=(c1y131),b=(化2y222),则 (1)ua+yb= (2)alb←台b=2a台. b≠0); (3)ab= (4)cos<a,b>-a lb
导航 四、向量的坐标运算 1.填空:已知a=(x1 ,y1 ,z1 ),b=(x2 ,y2 ,z2 ),则 (1)μa+vb= (μx1+vx2 ,μy1+vy2 ,μz1+vz2 ) ; (2)a∥b⇔b=λa⇔ x2 =λx1 ,y2 =λy1 ,z2 =λz1 (b≠0); (3)a·b= x1x2+y1 y2+z1 z2 ; (4)cos<a,b>= 𝒂·𝒃 |𝒂||𝒃| = 𝒙𝟏 𝒙𝟐 +𝒚𝟏 𝒚𝟐 +𝒛𝟏 𝒛𝟐 𝒙𝟏 𝟐 +𝒚𝟏 𝟐 +𝒛𝟏 𝟐 𝒙𝟐 𝟐 +𝒚𝟐 𝟐 +𝒛𝟐 𝟐

导航、 2.做一做:若a=(1,1,1),b=(-1,0,-2),则(a+b)b=一 解析:.a+b=(0,1,-1), .∴(a+b)b=2. 答案:2
导航 2.做一做:若a=(1,1,1),b=(-1,0,-2),则(a+b)·b= . 解析:∵a+b=(0,1,-1), ∴(a+b)·b=2. 答案:2

导航 思考辨析】 判断正误(正确的画“V”,错误的画“×”) (1)0与任何向量平行,与任何向量垂直.( (2)空间中任何两个非零向量都共面.( (3)若alb,则a与b同向.( (4)若ab<0,则<a,b>为钝角.( (5)若M1,2,3),N(2,1,2),则MN=(-1,1,1).( (6)若a=(-2,1,4),b=(-1,-1,5),则2a-b=(-3,3,3).(
导航 【思考辨析】 判断正误.(正确的画“√”,错误的画“×”) (1)0与任何向量平行,与任何向量垂直.( √ ) (2)空间中任何两个非零向量都共面.( √ ) (3)若a∥b,则a与b同向.( × ) (4)若a·b<0,则<a,b>为钝角.( × ) (5)若M(1,2,3),N(2,1,2),则 =(-1,1,1).( × ) (6)若a=(-2,1,4),b=(-1,-1,5),则2a-b=(-3,3,3).( √ ) 𝑴 𝑵
导期 课堂·重难突破 探究一空间向量的线性运算 【例1】如图,在长方体ABCD-A1B1CD中,O为AC的中点, D (1)化简A10-2AB-2AD= B (2)用AB,AD,AA表示0C, 则0C= B 分析:结合图形,灵活应用三角形法则和平行四边形法则求解
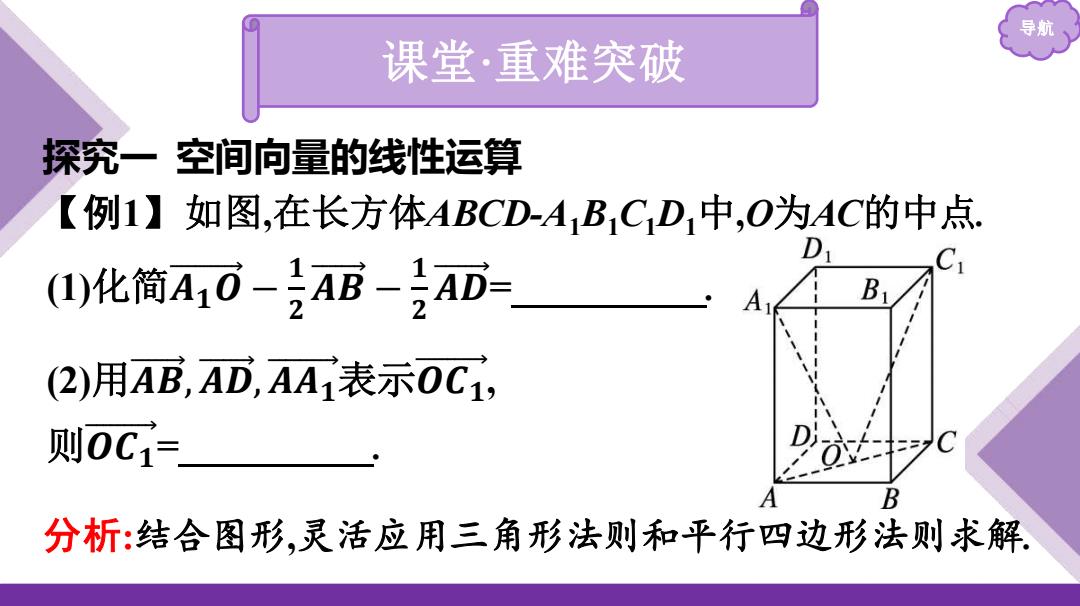
导航 (1)化简𝑨 𝟏 𝑶 − 𝟏 𝟐 𝑨 𝑩 − 𝟏 𝟐 𝑨 𝑫 = . (2)用𝑨 𝑩 ,𝑨 𝑫 ,𝑨𝑨𝟏 表示𝑶𝑪𝟏 , 则𝑶𝑪𝟏 = . 课堂·重难突破 探究一 空间向量的线性运算 【例1】如图,在长方体ABCD-A1B1C1D1中,O为AC的中点. 分析:结合图形,灵活应用三角形法则和平行四边形法则求解