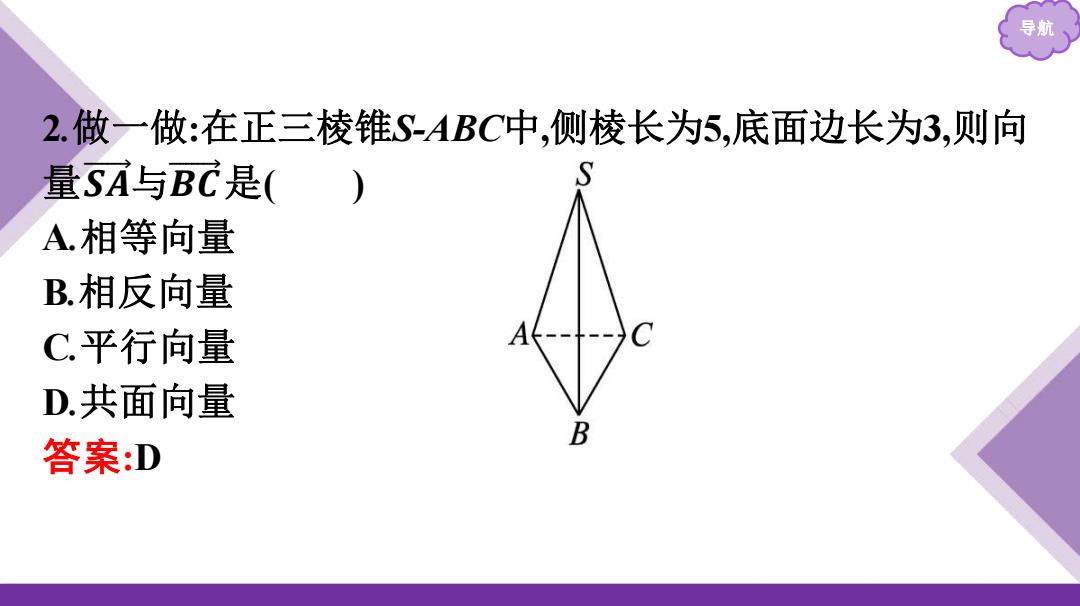
导 2.做一做:在正三棱锥SABC中,侧棱长为5,底面边长为3,则向 量SA与BC是( A.相等向量 B.相反向量 C平行向量 A-- D.共面向量 B 答案:D
导航 2.做一做:在正三棱锥S-ABC中,侧棱长为5,底面边长为3,则向 量 是( ) A.相等向量 B.相反向量 C.平行向量 D.共面向量 答案:D 𝑺 𝑨 与𝑩 𝑪

导航 二、空间向量的有关定理 【问题思考】 1填表: 定理 内容 共线向量 如果a0,且bla,则存在唯一的实数2,使得b=a 基本定理 共面向 若两个向量a,b不共线,则向量a,b,c共面的充要条 量定理 件是,存在唯一的实数对化,y),使c=xyER
导航 二、空间向量的有关定理 【问题思考】 1.填表: 定理 内容 共线向量 基本定理 如果a≠0,且b∥a,则存在唯一的实数λ,使得b=λa 共面向 量定理 若两个向量a,b不共线,则向量a,b,c共面的充要条 件是,存在唯一的实数对(x,y),使c= xa+yb ,x,y∈R

导期 定理 内容 平面向量 若平面内两个向量a与b不共线,则对该平面内任意 基本定理 一个向量c,存在唯一的实数对(c,y),使得c=xa+yb 定理:如果空间中的三个向量a,b,c不共面,那么对 空间中任意一个向量,存在唯一的有序实数组 空间向量 化y,z)使得p= 基本定理 推论:设O,A,B,C是不共面的四点,则对平面ABC内 任一点P都存在唯一的三个有序实数x,y,z,使 OP=xOA+vOB+zOC,x+y=1
导航 定理 内容 平面向量 基本定理 若平面内两个向量a与b不共线,则对该平面内任意 一个向量c,存在唯一的实数对(x,y),使得c=xa+yb 空间向量 基本定理 定理:如果空间中的三个向量a,b,c不共面,那么对 空间中任意一个向量p,存在唯一的有序实数组 (x,y,z)使得p= xa+yb+zc . 推论:设O,A,B,C是不共面的四点,则对平面ABC内 任一点P都存在唯一的三个有序实数x,y,z,使 𝑶 𝑷 =x𝑶 𝑨 +y𝑶 𝑩 +z𝑶 𝑪 ,且 x+y+z=1
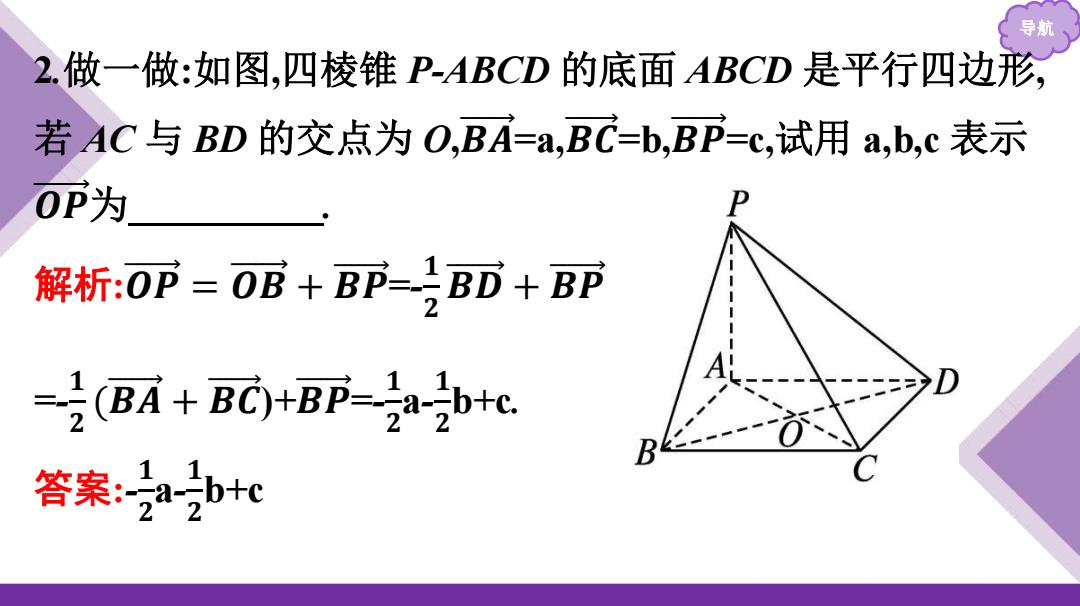
导航 2.做一做:如图,四棱锥P-ABCD的底面ABCD是平行四边形, 若AC与BD的交点为O,BA=a,BC=b,BP=c,试用a,b,c表示 OP为 解析:OP=OB+BP-BD+BP -(BA+BC)+BF-ia-b+c. 答案:2ab+c
导航 2.做一做:如图,四棱锥 P-ABCD 的底面 ABCD 是平行四边形, 若 AC 与 BD 的交点为 O,𝑩 𝑨 =a,𝑩 𝑪 =b,𝑩 𝑷 =c,试用 a,b,c 表示 𝑶 𝑷 为 . 解析:𝑶 𝑷 = 𝑶 𝑩 + 𝑩 𝑷 =- 𝟏 𝟐 𝑩 𝑫 + 𝑩 𝑷 =- 𝟏 𝟐 (𝑩 𝑨 + 𝑩 𝑪 )+𝑩 𝑷 =- 𝟏 𝟐 a- 𝟏 𝟐 b+c. 答案:- 𝟏 𝟐 a- 𝟏 𝟐 b+c

导 三、两个向量的数量积 【问题思考】 1.填空:(1)两个向量的夹角:空间中,给定两个非零向量a,b,任 意在空间中选定一点0,作0A=a,0B=b,则 叫作a与b的 夹角,记作,其范围是 若<a,b>=2,则 (2)两向量的数量积:ab= 3)空间向量的数量积的性质: ①aLb台 ;②aa==a2;③ab ;④2a)b= ⑤ab=(交换律);⑥(a+b)c=ac+bc(分配律)
导航 三、两个向量的数量积 【问题思考】 1.填空:(1)两个向量的夹角:空间中,给定两个非零向量a,b,任 意在空间中选定一点O,作 ,则∠AOB叫作a与b的 夹角,记作<a,b>,其范围是[0,π];若<a,b>= ,则a⊥b . (2)两向量的数量积:a·b=|a||b|cos<a,b> . (3)空间向量的数量积的性质: ①a⊥b⇔ a·b=0;②a·a= |a| 2 =a 2 ;③|a·b|≤ |a||b|;④(λa)·b=λ(a·b); ⑤a·b=b·a(交换律);⑥(a+b)·c=a·c+b·c(分配律). 𝑶 𝑨 =a,𝑶 𝑩 =b 𝛑 𝟐