
优化试验设计与数据分析 第七章单纯形优北法 cmese,uestc 本章主要内容 单纯形方法的基本数学原理 0 基本单纯形:双因素基本单纯形、直角单纯形、双水平单 纯形优化推进方法。 改进单纯形、加权形心法、控制加强形心法。 灵活运用各种单纯形的改进方法。 School of Microelectronics and Solid-State Electronics
School of Microelectronics and Solid-State Electronics 1 优化试验设计与数据分析 本章主要内容 · 单纯形方法的基本数学原理。 · 基本单纯形:双因素基本单纯形、直角单纯形、双水平单 纯形优化推进方法。 · 改进单纯形、加权形心法、控制加强形心法。 · 灵活运用各种单纯形的改进方法
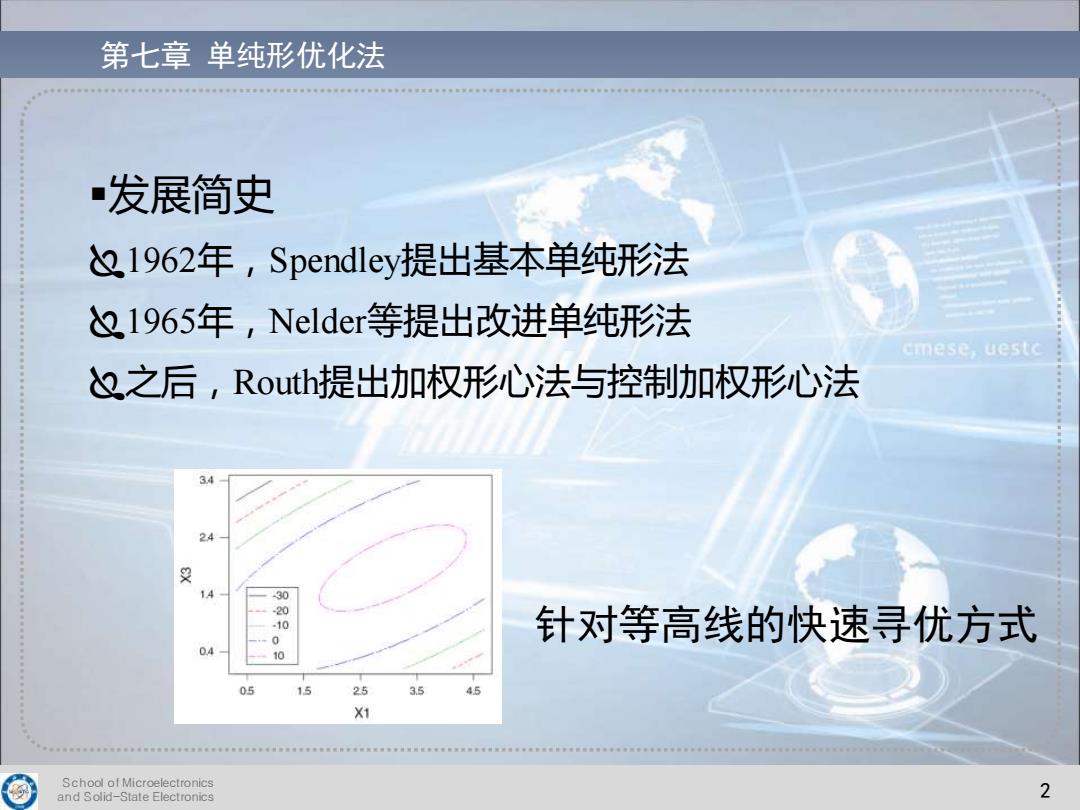
第七章单纯形优化法 发展简史 点1962年,Spendley提出基本单纯形法 、1965年,Nelder等提出改进单纯形法 cmese,uestc 之后,Routh提出加权形心法与控制加权形心法 34 14 30 0 针对等高线的快速寻优方式 04 05 15 25 3 45 X1 School of Microelectronics and Solid-State Electronics 2
School of Microelectronics and Solid-State Electronics 2 第七章 单纯形优化法 ▪发展简史 1962年,Spendley提出基本单纯形法 1965年,Nelder等提出改进单纯形法 之后,Routh提出加权形心法与控制加权形心法 针对等高线的快速寻优方式

第七章单纯形优化法 基本单纯形 一、双因素基本单纯形法 如果我们有一个试验设计,只选有两个影 uestc 响因素,即因素数为2。分别取值a1和a2作 为试验的初点。记为A(a1,a2)。对其余两个 点分别设为B和C,再设三角形的边长为a( 步长)。那么B、C点就可以计算出来 School of Microelectronics and Solid-State Electronics 3
School of Microelectronics and Solid-State Electronics 3 第七章 单纯形优化法 基本单纯形 一、双因素基本单纯形法 如果我们有一个试验设计,只选有两个影 响因素,即因素数为2。分别取值a1和a2作 为试验的初点。记为A(a1 ,a2 )。对其余两个 点分别设为B和C,再设三角形的边长为a( 步长)。那么B、C点就可以计算出来

第七章单纯形优化法 假设AB、AC、BC间距均为a,等边三角形可以算出B点为: B-(aj+p,az+q) 根据对称性可知: C=(aj+q,a2+p) cmese,uestc 可以根据等边三角形性质解得: √5-1 9 a 2√2 (9-1)) √3+1 D= a 2W2 School of Microelectronics and Solid-State Electronics 4
School of Microelectronics and Solid-State Electronics 4 第七章 单纯形优化法 假设AB、 AC、BC间距均为a,等边三角形可以算出B点为: B=(a1+p, a2+q) 根据对称性可知: C=(a1+q, a2+p) 可以根据等边三角形性质解得: 3 1 2 2 (9 1) 3 1 2 2 q a p a − = − + =
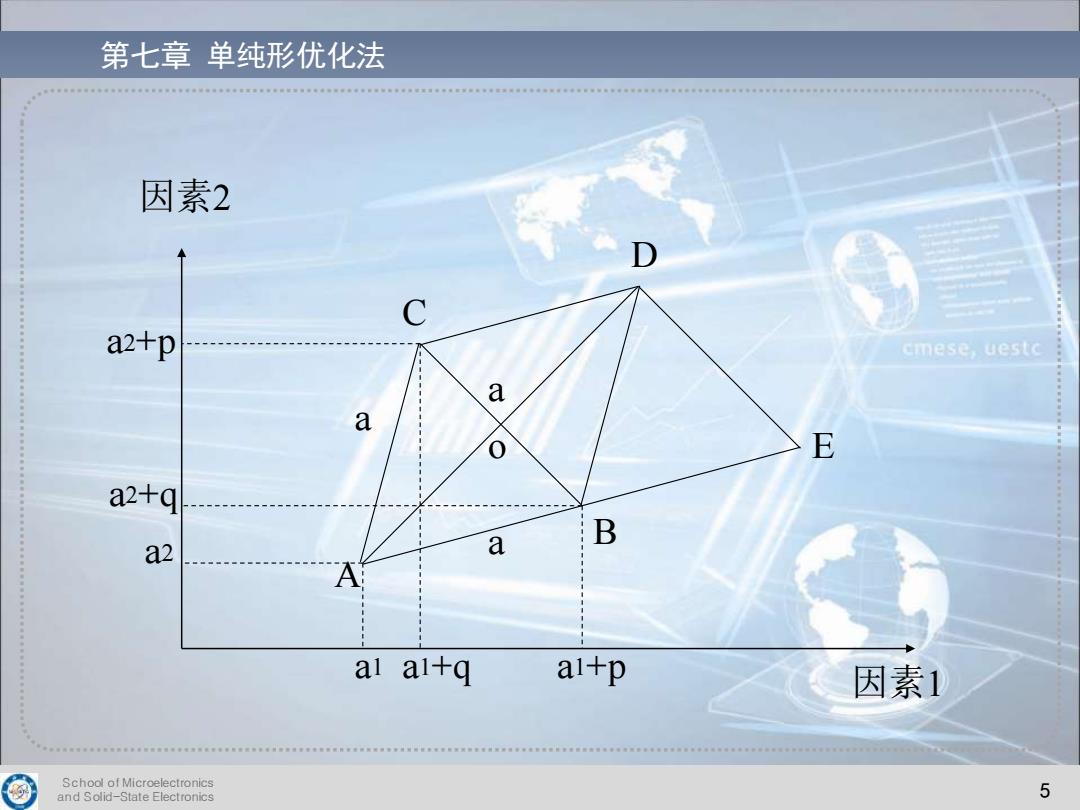
第七章单纯形优化法 因素2 a2+p cmese,uestc a a E a2+q B a2 a A al ai+q ai+p 因素1 School of Microelectronics and Solid-State Electronics 5
School of Microelectronics and Solid-State Electronics 5 第七章 单纯形优化法 a2+p a2+q a2 a1 a1+q a1+p 因素2 因素1 A B C D o E a a a