
因平行向量可平移到同一直线上,故两向量平行又称 两向量共线 若k(3)个向量经平移可移到同一平面上,则称此k 个向量共面 HIGH EDUCATION PRESS
因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面

二、向量的线性运算 1.向量的加法 2.向量的减法 3.向量与数的乘法 定理1. HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、向量的线性运算 1. 向量的加法 机动 目录 上页 下页 返回 结束 2. 向量的减法 3. 向量与数的乘法 定理1

二、向量的线性运算 1.向量的加法 平行四边形法则: (@+B)+c a+而 a+(B+c) a+不 三角形法则: a+b a 运算规律:交换律 a+b-b+a 结合律 (a+b)+c-a+(B+c)-a+b+c 三角形法则可推广到多个向量相加 HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . 机动 目录 上页 下页 返回 结束 b b a + b = b + a ( a + b) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) ( a + b) + c a a a + b a + b
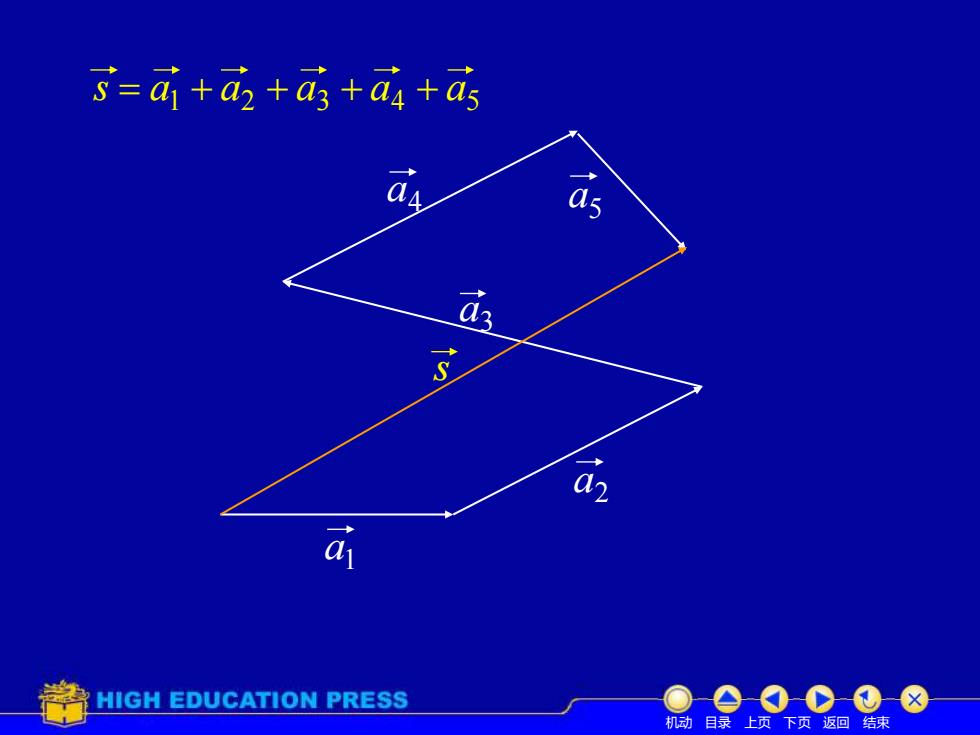
s-a+a +as+as +as 05 HIGH EDUCATION PRESS 机动目录上页下页返回结束
机动 目录 上页 下页 返回 结束 s a3 a4 5 a a2 a1 1 2 3 4 5 s = a + a + a + a + a

2.向量的减法 万-a=b+(-a b-a 特别当b=a时,有 a a-a-a+(-a)-0 三角不等式 a+b s a+b a+b a-bs a+b HIGH EDUCATION PRESS 机动目录上页下页返回结束
2. 向量的减法 三角不等式 机动 目录 上页 下页 返回 结束 a