
第二节 第五章 平面及其方程 一、 平面的点法式方程 二、 平面的一般方程 三、平面的截距式方程 四、平面与平面、点与平面的关系 HIGH EDUCATION PRESS 下页返回结束
第二节 一、平面的点法式方程 二、平面的一般方程 四 、平面与平面、点与平面的关系 机动 目录 上页 下页 返回 结束 平面及其方程 第五章 三、平面的截距式方程

一、平面的点法式方程 设一平面通过已知点M(x,y%,二,)且垂直于非零向 量n=(A,B,C),求该平面Π的方程 任取点M(x,y,z)eⅡ,则有 MM⊥元 故 MoM.n=0 MoM=(x-x0,y-o,2-20) A(x-xo)+B(y-y%)+C(2-2o)=0 称①式为平面Π的点法式方程,称为平面Ⅱ的法向量. HIGH EDUCATION PRESS 机动目录上页下页返回结束
z y x o M0 n ① 一、平面的点法式方程 ( , , ) 0 0 0 0 设一平面通过已知点 M x y z 且垂直于非零向 A(x − x0 ) + B(y − y0 ) +C(z − z0 ) = 0 M 称①式为平面的点法式方程, 求该平面的方程. 任取点M (x, y,z), 法向量. 量 n = (A , B, C), M0M ⊥n M0M n = 0 则有 故 称 n为平面 的 机动 目录 上页 下页 返回 结束

例1.求过点M(2,3,1)且与n=(-1,-2,0) 垂直的平面Π的方程 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例1.求过点 垂直的平面 的方程. 机动 目录 上页 下页 返回 结束 且与
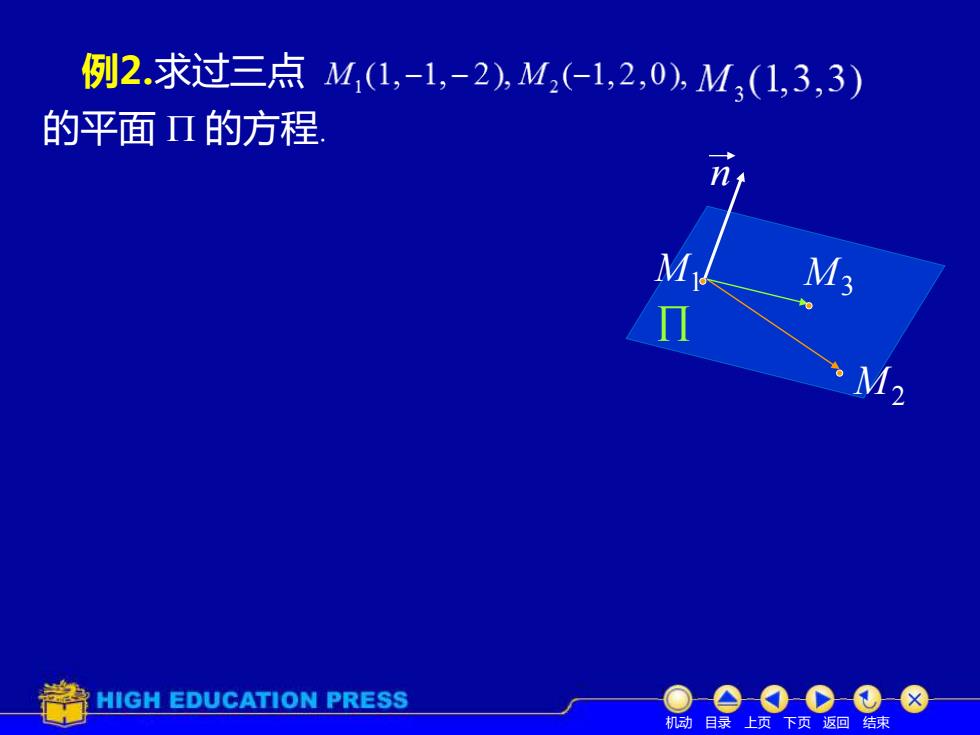
例2.求过三点M,(1,-1,-2),M2(-1,2,0),M,(1,3,3) 的平面Π的方程 M M3 M2 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例2.求过三点 M1 M2 M3 的平面 的方程. n 机动 目录 上页 下页 返回 结束

说明:一般情况:过三点Mk(xk,yk,k)(k=1,2,3) 的平面方程为 x-为y-片2-21 X2-X1y2-y122-21 =0 3-x13-1 23-21 上述平面的三点式方程也可写成 x-2y+12-4 -3 -6 =0 -23 -1 HIGH EDUCATION PRESS 机动目录上页下页返回结束
一般情况 : 过三点 M (x , y ,z ) (k =1,2,3) k k k k 的平面方程为 说明: 机动 目录 上页 下页 返回 结束 上述平面的三点式方程也可写成 0 2 3 1 3 4 6 = − − − − x − 2 y +1 z − 4