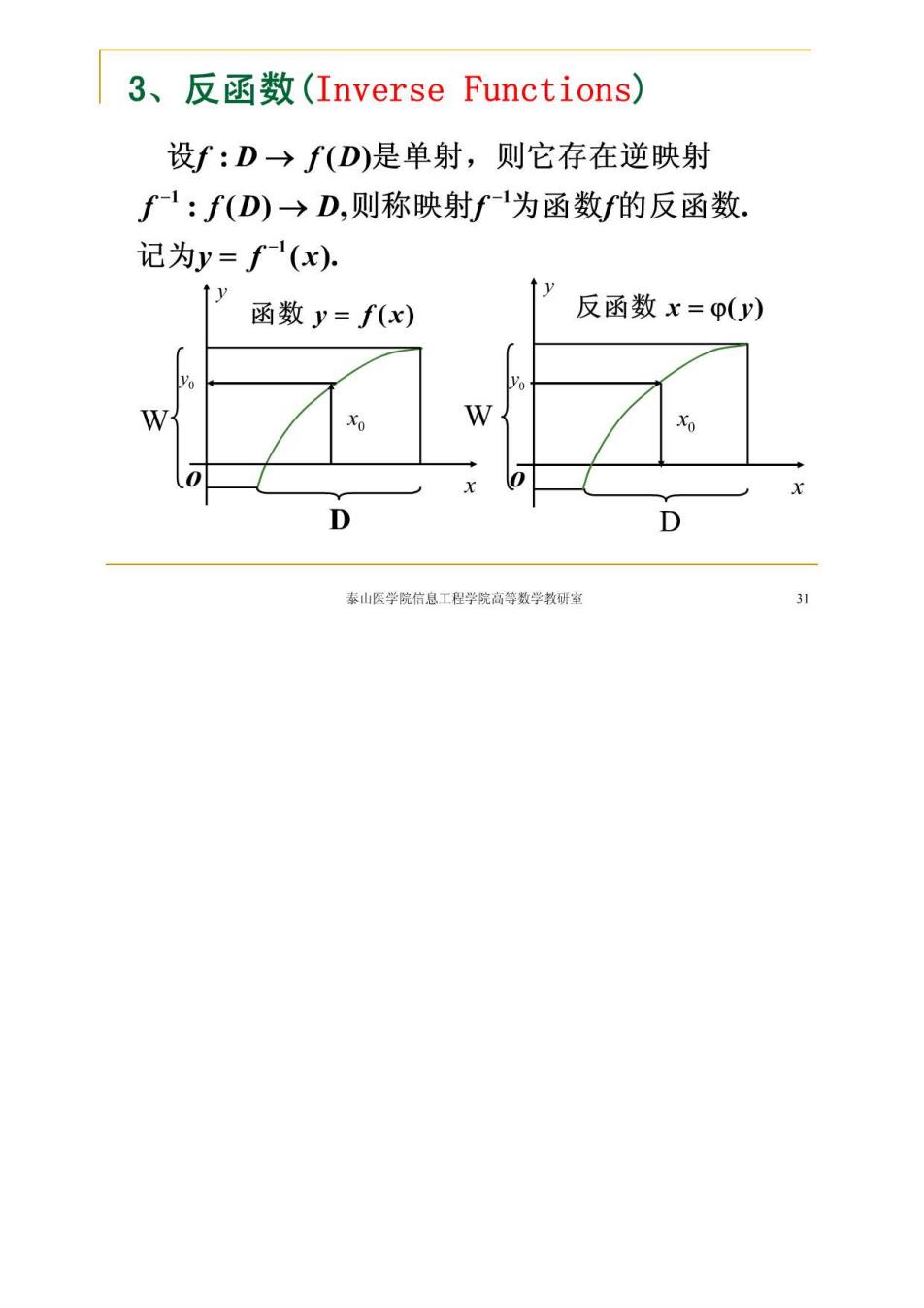
3、反函数(Inverse Functions) 设f:D→f(D)是单射,则它存在逆映射 f:f(D)→D,则称映射f为函数f的反函数. 记为y=f(x), ↑y y 函数y=f(x) 反函数x=p(y) W W 0 D 泰山医学院信息工程学院高等数学教研室

反函数yラφ(x) Q(b,a) 直接函数y=f(x) P(a,b 直接函数与反函数的图形关于直线y=x对称. 结论:单调函数f必存在单调的反函数,且 具有与相同的单调性。 素山医学院信息工程学院高等数学教研室 3

4、复合函数(composite function) 所谓复合函数就是把两个或两个以上的函数 组合成一个新的函数, 如:设y=√,u=1-x2,→y=V1-x2 定义:设函数y=f(w)的定义域D,而函数 4=(x)的值域为乙。,若乙,cD1,则称函数 y=fIp(x川为x的复合函数. x←自变量,←中间变量,y←因变量, 素山医学院信息工程学院高等数学教研室 33

注意:1)g和f构成复合函数的条件是:g的值域必须含在f 的定义域内。 例如y=√u,u=tan构成复合函数,其定义域 D={xkπ≤x<k+ 2)不是任何函数都可以复合成一个函数。 例如y=arcsin4,u=2+x不能构成复合函数。 3)复合函数可以由两个以上的函数经过复合构成 x 例如y=cot2y=Vm,M=cot,v三 2 泰山医学院信息工程学院高等数学教研室 34

5、函数的运算 设函数f(x),g(x)的定义域为D,D, D=DOD,≠空集,则有下列运算: 和(差)f±g:(f±g)x)=f(x)±g(x),x∈D 积f·g: (f·g)(x)=f(x)g(x),x∈D 商 I. ()-f)xeD()=0xE g(x) 泰山医学院信息工程学院高等数学教研室 35