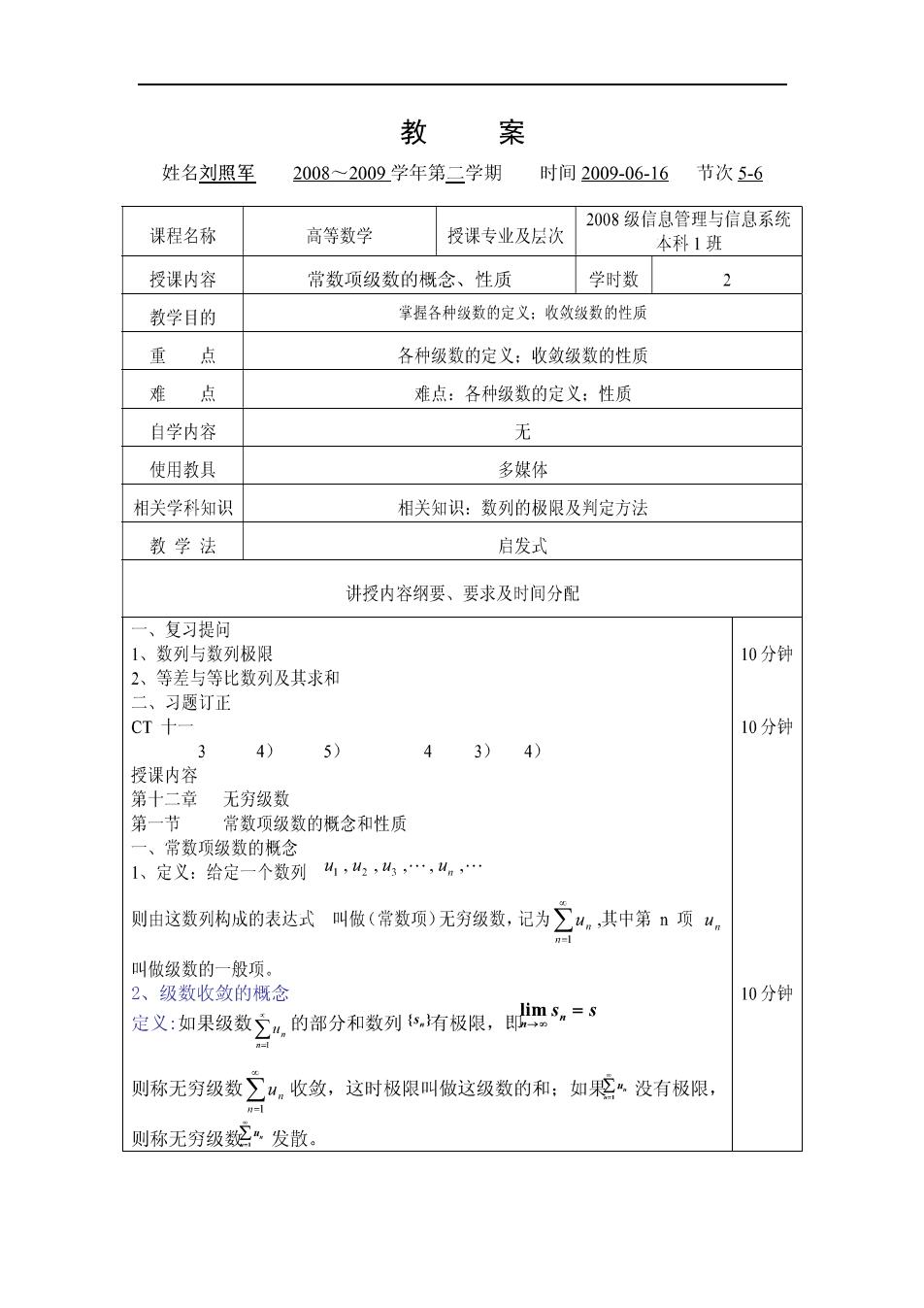
彭 案 姓名刘照军 2008~2009学年第二学期 时间2009-06-16节次5-6 2008级信息管理与信息系统 课程名称 高等数学 授课专业及层次 本科1班 授课内容 常数项级数的概念、性质 学时数 2 教学目的 掌握各种级数的定义:收敛级数的性质 重点 各种级数的定义:收敛级数的性质 难点 难点:各种级数的定义:性质 自学内容 无 使用教具 多媒体 相关学科知识 相关知识:数列的极限及判定方法 教学法 启发式 讲授内容纲要、要求及时间分配 复习提问 1、数列与数列极限 10分钟 2、等差与等比数列及其求和 二、习题订正 CT十 10分, 3 4) 5) 43)4) 授课内容 第十二章无穷级数 第一节 常数项级数的概念和性质 一、常数顶级数的概念 1、定义:给定一个数列4,山,.,4n 则由这数列构成的表达式叫做(常数项)无穷级数,记为∑“。,其中第n项“。 叫做级数的一般顶。 2、级数收敛的概念 10分钟 定义:如果级数空,的部分和数列有极限,四。= 则称无穷级数∑“。收敛,这时极限叫做这级数的和:如没有极限, 则称无穷级·发散

讲授内容纲要、要求及时间分配(附页) 3、应用 例1讨论级数元ag=a+a叫+ag++ag+.的敛散性。 5分钟 = 例2证明级数1+2+3+.+n+.是发散的。 10分钟 例3到定级数1223 1 1 1 .+ n(n+D +.的敛散性 5分钟 二、收敛级数的基本性质 性质1如果级数上,收效于和s,则级数∑仙,也收敛,日其和为ks 5分钟 性质2如果级数空、立,分别收敛于s和t则级数空,士 5分钟 也收敛,且其和为s±t 性质3、在级数中去掉、加上或改变有限项,不会改变级数的收敛性。 5分钟 性质4如果级数收敛,则对这级数的项任意加括号后所成的 5分钟 级数收敛。特别注意:此结论的逆定理不成立。 性质5(级数收敛的必要条件) 5分钟 如果级数立山。收敛,则它的一般项趋于零,即m”,=0 注意:级数的一般项趋于零并不是级数收敛的充分条件 三、柯西审敛法 定理(柯西审敛法),级数收敛的充要条件是:对于任意给定的E,总10分钟 存在自然数N,当>N时,对于任意的自然数p,都有下式成立 ul+u2+.+u<E 4列定级数三的数敏 5分钟 、小结:本将主要讲述了级数的定义、性质及审敛判别法 5分钟 1 正项级数的性质 调和级数的证明 五、作业 CT12-1P254 23) 4) 45 390 5分钟
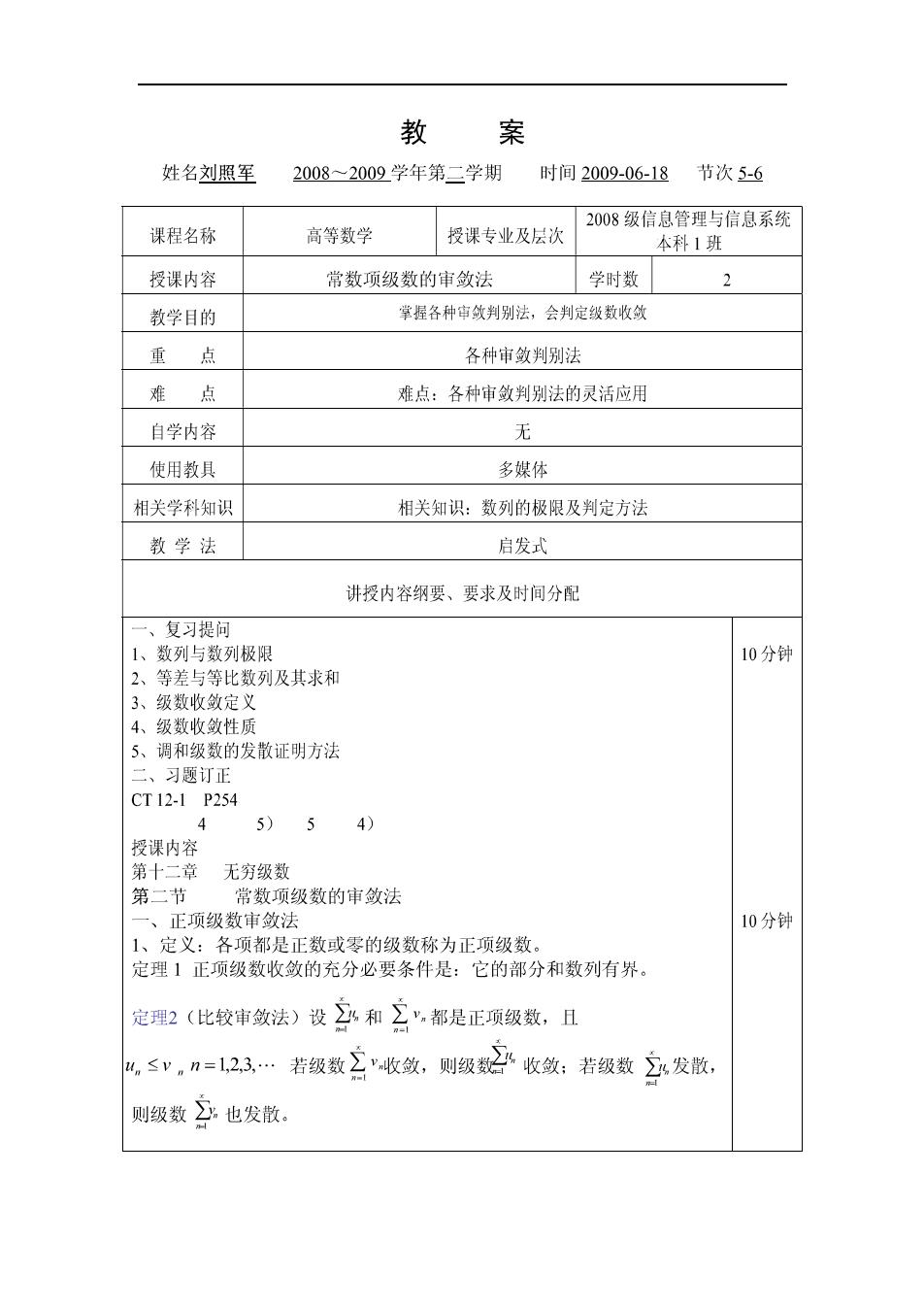
教 案 姓名刘照军 2008~2009学年第二学期 时间2009-06-18节次5-6 2008级信息管理与信息系统 课程名称 高等数学 授课专业及层次 本科1班 授课内容 常数项级数的审敛法 学时数 2 教学目的 掌握各种审敛判别法,会判定级数收敛 重点 各种审敛判别法 难点 难点:各种审敛判别法的灵活应用 自学内容 无 使用教具 多媒体 相关学科知识 相关知识:数列的极限及判定方法 教学法 启发式 讲授内容纲要、要求及时间分配 复习提问 1、数列与数列极限 10分钟 2、等差与等比数列及其求和 3、级数收敛定义 4。经断收的性质 5、调和级数的发散证明方法 二、习题订正 CT12-1P254 4 5)5 4) 授课内容 第十二章无穷级数 第二节 常数项级数的审敛法 、正项级数审敛法 10分钟 1、定义:各项都是正数或零的级数称为正项级数。 定理1正项级数收敛的充分必要条件是:它的部分和数列有界。 定理2(比较审敛法)设和∑,都是正项级数,且 以,≤v.n=123.若级数立收敛,则级2收敛:若级数立发散, 则级数∑也发散

讲授内容纲要、要求及时间分配(附页) 2、应用 10分钟 例1讨论1 11 1 2+3+.+ +.级数的收敛性,其中常数p>0 例2证明级数了1 是发散的 台Vn(n+万 3、比较审敛法的极限形式 10分钟 定理3(比较审敛法的极限形式)没2和三都是正项级数。 )如果m兰=①≤1<+)且三”,级数收敛则级2“。收敛: ②如果m长=或兰m且公级数发散则级数立发放。 2和 4、应用 10分钟 定理4(比值审敛法,达朗贝尔判别法) 设子为正项级数,如果m=P则当P<时级数收敛。 当p>1或当一= 时,级数发散 当P=1时级数可能收敛也可能发散。 例4证明1+23*+123a-* 1 1 例5判 收收,计污素 1010+10 定理5(根值审敛法,柯西判别法) 10分钟 设立纳下项袋数,如哭m瓦,=p 侧6判断级数22+6少 的敛散性。 定理6(极限审敛法)设∑”,为正项级数, 10分钟 ()如果mm,=>0mm=o,立,发散。 (2如果p>1,而imm,=10≤1<+四)收敛。则立,收敛

讲授内容纲要、要求及时间分配(附页) 例7判定级数l+)的收敛性. 例8判定级数∑n+10-c0s马的收敛性 二、 交错级数及其审敛法 10分钟 1、定义:交错级数是指这样的级数,它的各项是正负交错 的,从而可以写成的形式:4,一4,+4-4+. 或 一+一%+一.其中,4,.都是正数。 定理7(莱布尼茨定理,交错级数审敛法) 如果交错级数∑-)%满足条件:,≥1(=1,2,. m,=0,则级数收敛,且其和s≤4,其余项的绝对值5从 三、绝对收敛与条件收敛 1、定义:设为常数项级数,如果它的各项的绝对值所构成的 10分钟 正项级数立a收敛,则称级数”,。绝对收敛: 如果级数立4,收敛,而级数发散则称级数,条件收敛 定理8 如果级数, 绝对收敛 则级数 必定收 *定理9绝对收敛级数经改变项的位置后构成的级数也收敛, 且与原级数有相同的和。 例9判定级数了血n口的收敛性。 合n2 例10判定级数卫(-少是0+的收敛性 四、小结:本将主要讲述了级数的定义、性质及审敛判别法 1、正项级数的性质 5分钟 2、 正项级数的比较判别法:自身判别法 3、交错级数的收敛判别法 4、条件收敛与绝对收敛 5、调和级数与p-级数的收敛判别 五、作业 5分钟 CT12-2P206 1 4)5) 2 33) 4) 3) 4)5)