
几种常见的离散型随机变量的数学期望 1.0-1分布的数学期望 0”。 E(X)=p. 2.二项分布的数学期望 P(X=k)Chp*(1-p)"k k=0.1,n E(X)=np. 2024年8月27日星期二 12 目录○ 上页 下页 返回
2024年8月27日星期二 12 目录 上页 下页 返回 几种常见的离散型随机变量的数学期望 1. 0-1分布的数学期望 P p − p X 1 1 0 E(X) =p. 2. 二项分布的数学期望 P X k C p p k n k k n k n { = } = (1− ) = 0.1,. − E(X) =np
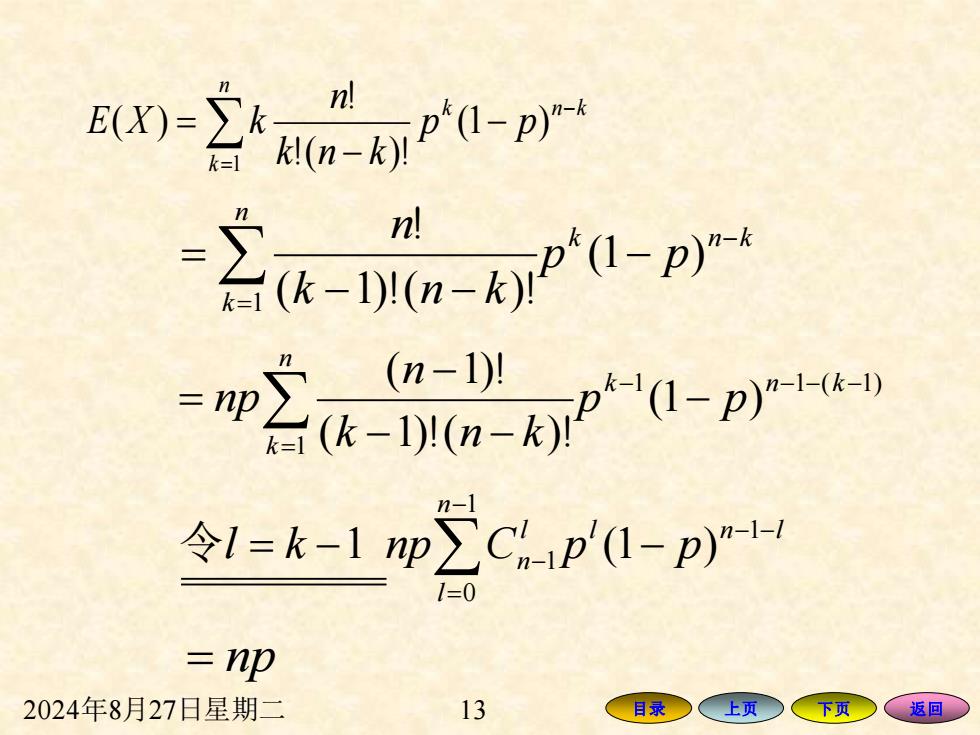
8-2uarn-pr n 含 空aPn (n-1)y 令1=k-1p∑Cp'I-p)- 1=0 =np 2024年8月27日星期二 13 目录○ 、上页 下页 返回
2024年8月27日星期二 13 目录 上页 下页 返回 k n k n k p p k n k n − = − − − = (1 ) ( 1)!( )! ! 1 1 1 ( 1) 1 (1 ) ( 1)!( )! ( 1)! − − − − = − − − − = k n k n k p p k n k n np = np l n l n l l l k np Cn p p − − − = = − − − 1 1 0 1 令 1 (1 ) = − − − = n k k n k p p k n k n E X k 1 (1 ) !( )! ! ( )

3.泊松分布的数学期望 X-P4x=k=e,k=012 →E=229 台(k-1) 4.几何分布的数学期望 XP{X=k}=p(1-p)-,k=0,1,2, →E(X)=∑p(1-p) K=1 =p(1+2q+3q2+.) (q=1-p) g=1 2024年8月27日星期(1-q)2p14 目录○ 上页 下页 返回
2024年8月27日星期二 14 目录 上页 下页 返回 3. 泊松分布的数学期望 , 0, 1, 2, . ! ~ { = } = = − e k k X P X k k 1 0 1 ( ) ; ! ( 1)! k k k k E X k e e k k − − − = = = = = − 4. 几何分布的数学期望 ~ { } (1 ) , 0,1, 2, . 1 = = − = − X P X k p p k k 1 1 ( ) (1 )k K E X kp p − = = − 2 1 (1 ) p q p = = − 2 = + + + = − p q q q p (1 2 3 .) ( 1 )