
第三节 依方差和相关象数 如果两个随机变量是相互独立,则有 E{LX-(EX)][Y-E(Y)]}=0 如果两个随机变量是不相互独立,则有 E[X-(EX)[Y-E(Y)]}≠0 这说明它们存在一定的相关关系. 问题:如何描述两个随机变量之间相互关系。 2024年8月27日星期二 1 目录 上页 下页 返回
2024年8月27日星期二 1 目录 上页 下页 返回 第三节 协方差和相关系数 如果两个随机变量是相互独立,则有 E X EX Y E Y [ ( )][ ( )] 0 − − = 如果两个随机变量是不相互独立,则有 E X EX Y E Y [ ( )][ ( )] 0 − − 这说明它们存在一定的相关关系. 问题:如何描述两个随机变量之间相互关系

一、协方差的定义及计算公式 定义:随机变量X和Y的协方差Cov(X,)定义为 Cov(X,Y)=E[X-(EX)]Y-E(Y)] 当DX),D(>0时, Cov(X,Y) PW=DD西 称为随机变量X和Y的相关系数。 2024年8月27日星期二 2 目录○ (上页下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 一 、协方差的定义及计算公式 定义:随机变量X和Y的协方差Cov(X,Y)定义为 Cov X Y E X EX Y E Y ( , ) [ ( )][ ( )] = − − 当D(X), D(Y)>0 时, ( , ) ( ) ( ) XY Cov X Y D X D Y = 称为随机变量X和Y的相关系数

计算公式: Cov(X,Y)=E(XY)-E(X)E(Y) 证明:Cov(X,Y)=E{X-(EX)I[Y-E(Y] =EXY-XE(Y)-YE(X)+E(X)E(Y) =E(XY)-E(X)E(Y)-E(Y)E(X)+E(X)E(Y) =E(XY)-E(XE(Y) 2024年8月27日星期二 3 目录上页下页○ 返回
2024年8月27日星期二 3 目录 上页 下页 返回 计算公式: Cov(X,Y)=E(XY)―E(X) E(Y) 证明: Cov X Y E X EX Y E Y ( , ) [ ( )][ ( )] = − − = − − + E XY XE Y YE X E X E Y ( ) ( ) ( ) ( ) = − − + E XY E X E Y E Y E X E X E Y ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − E XY E X E Y ( ) ( ) ( )

性质: 1.Cov(Y,Y)=Cov(Y,X) 2.Cov(X,X)=D(X) 3.D(X+Y)=D(X)+D(Y)+2Cov(X,Y) 4.Cov(ax,bY)=abCov(X,Y) 5.Cov(X+X2,Y)=Cov(Xj,Y)+Cov(X2,Y) 6.若随机变量X和Y相互独立,则协方差为零。 但逆命题不成立,即协方差为零,X和Y不一定相互独立。 2024年8月27日星期二 4 目录 上页 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 性质: 1. Cov X Y Cov Y X ( , ) ( , ) = 2. Cov X X D X ( , ) ( ) = 3. D X Y D X D Y Cov X Y ( ) ( ) ( ) 2 ( , ) + = + + 4. Cov aX bY abCov X Y ( , ) ( , ) = 5. 1 2 1 2 Cov X X Y Cov X Y Cov X Y ( , ) ( , ) ( , ) + = + 6. 若随机变量X和Y相互独立,则协方差为零。 但逆命题不成立,即协方差为零,X和Y不一定相互独立
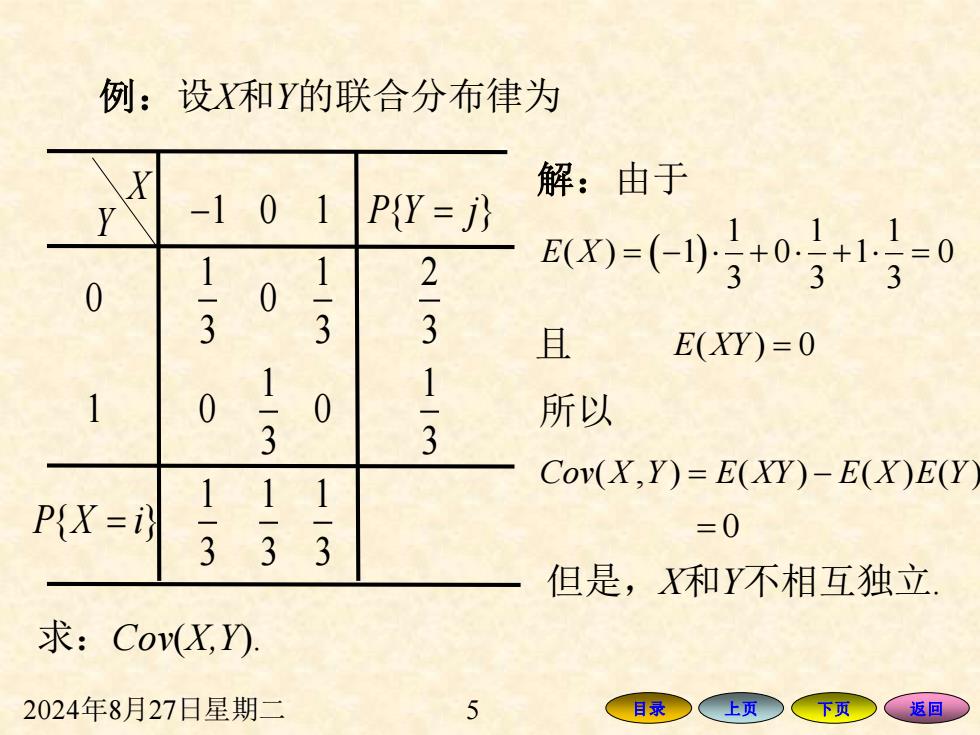
例:设和Y的联合分布律为 解:由于 -1 0 PY=j) +1.}-0 1 2 E(X)=(-)5+0 3 3 0 3 3 3 且 E(XY=0 1 1 0 0 所以 3 3 Cov(X,Y)=E(XY)-E(X)E(Y 1 11 P{X=议 33 =0 3 但是,X和Y不相互独立 求:Cov(X,Y) 2024年8月27日星期二 5 目录○ 、上页 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 X Y 1 0 1 { } 1 1 2 0 0 3 3 3 1 1 1 0 0 3 3 1 1 1 { } 3 3 3 P Y j P X i − = = 例:设X和Y的联合分布律为 求:Cov(X,Y). 解:由于 ( ) 1 1 1 ( ) 1 0 1 0 3 3 3 E X = − + + = 且 E XY ( ) 0 = 所以 Cov X Y E XY E X E Y ( , ) ( ) ( ) ( ) = − = 0 但是,X和Y不相互独立