
第三节 随机变量的分布高数 与途续型随机变量 >分布函数的定义及其性质 >连续型随机变量的定义及其概率密度的性质 >几种重要的连续型随机变量 2024年8月27日星期二 目录 上页>下页 返回
2024年8月27日星期二 1 目录 上页 下页 返回 第三节 随机变量的分布函数 与连续型随机变量 ➢分布函数的定义及其性质 ➢连续型随机变量的定义及其概率密度的性质 ➢几种重要的连续型随机变量

一、分布函数的定义及性质 由于P(x,<X≤x2)=P(X≤x2)-P(X≤x) 为此我们引入随机变量的分布函数的概念如下: 定义:设X是一个随机变量,x是任意实数,函数 F(x)=P(X≤x) 称为随机变量X的分布函数。 从而 P(x1<X≤x2)=P(X≤x2)-P(X≤x)=F(x2)-F(x) 也就是说,可以通过分布函数,计算随机变量落在任意 个区间的概率。 2024年8月27日星期二 2 目录 上页 下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 一、分布函数的定义及性质 由于 1 2 2 1 P x X x P X x P X x ( ) ( ) ( ) = − 为此我们引入随机变量的分布函数的概念如下: 定义:设X是一个随机变量,x是任意实数,函数 F x P X x ( ) ( ) = 称为随机变量X的分布函数。 从而 1 2 2 1 P x X x P X x P X x ( ) ( ) ( ) = − 2 1 = − F x F x ( ) ( ) 也就是说,可以通过分布函数,计算随机变量落在任意 一个区间的概率

不加证明地给出分布函数的一些性质: (1)(单调性)对于任意实数x1,x2,(x1<x2),有 F(x)≤F(x2) (2)(有界性)0≤F(x)≤1,limF(x)=0,limF(x)=1 F(-∞)=P{X≤-o}不可能事件 F(+o)=P{X≤+o}必然事件 (3)(右连续性)1imF(x)=F(x) x→x0 2024年8月27日星期二 3 目录 上页 下页 返回
2024年8月27日星期二 3 目录 上页 下页 返回 不加证明地给出分布函数的一些性质: (1)(单调性) 对于任意实数 x x x x 1 2 1 2 , ,( ) ,有 1 2 F x F x ( ) ( ) (2)(有界性) 0 ( ) 1, lim ( ) 0, lim ( ) 1 →− →+ = = x x F x F x F x (3)(右连续性) 0 0 lim ( ) ( ) x x F x F x → + = F P X ( ) { } − = − 不可能事件 F P X ( ) { } + = + 必然事件

例:若随机变量X的分布律为 X|1234 1 11 288 则随机变量的分布函数为 0, x<1 P{=1, 1≤x<2 F(x)={P{X=1+P{X=2} 2≤x<3 P{X=1+P{X=2+P{X=3} 3≤x<4 P{X=1+P{X=2}+P{X=3}+P{X=4}4≤x 2024年8月27日星期二 目录上页> 下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 例:若随机变量X的分布律为 1 2 3 4 1 1 1 1 4 2 8 8 k X p 则随机变量X的分布函数为 ( ) = F x 0, x 1 P X =1 , 1 2 x P X P X = + = 1 2 2 3 x P X P X P X = + = + = 1 2 3 3 4 x P X P X P X P X = + = + = + = 1 2 3 4 4 x
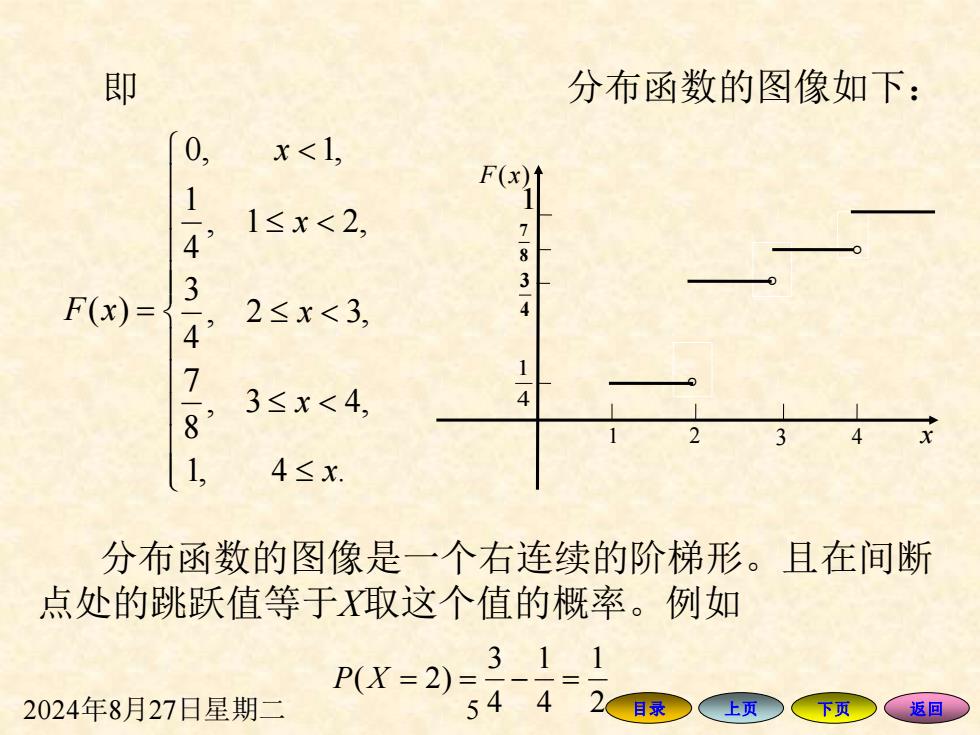
即 分布函数的图像如下: 0, x<1, F(x 14 1≤x<2, 7 3 F(x)= 2≤x<3, 4 8 3≤x<4, 4 1, 4≤x. 分布函数的图像是一个右连续的阶梯形。且在间断 点处的跳跃值等于取这个值的概率。例如 P(X=2) 311 2024年8月27日星期二 544 2日* 上页 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 即 0, 1, 1 , 1 2, 4 3 ( ) , 2 3, 4 7 , 3 4, 8 1, 4 . x x F x x x x = 分布函数的图像如下: 分布函数的图像是一个右连续的阶梯形。且在间断 点处的跳跃值等于X取这个值的概率。例如 。 。 1 。 4 7 8 3 4 1 1 2 3 4 F x( ) x 3 1 1 ( 2) 4 4 2 P X = = − =