
第四章随机变量的数字特征 问题的提出: 在实际应用中,除了需要了解随机变量的分布函数 外,我们更关心能够反映随机变量某些特征的指标。 例如: >在评定某地区粮食产量水平时,最关心的是平均产量 >在检查一批棉花的质量时,既需要注意纤维的平均长 度,又需要注意纤维长度与平均长度的偏离程度。 >考察广州市区居民的家庭收入情况,我们既要知道家 庭的年平均收入,又要研究贫富之间的差异程度。 2024年8月27日星期二 2 目录 、上页 下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 第四章 随机变量的数字特征 问题的提出: 在实际应用中,除了需要了解随机变量的分布函数 外,我们更关心能够反映随机变量某些特征的指标。 ➢考察广州市区居民的家庭收入情况,我们既要知道家 庭的年平均收入,又要研究贫富之间的差异程度。 例如: ➢在评定某地区粮食产量水平时,最关心的是平均产量 ➢在检查一批棉花的质量时,既需要注意纤维的平均长 度,又需要注意纤维长度与平均长度的偏离程度

第一节数学期望 一、离散型随机变量的数学期望 二、连续型随机变量的数学期望 三、数学期望的性质 2024年8月27日星期二 3 目录 上页> 下页 返回
2024年8月27日星期二 3 目录 上页 下页 返回 第一节 数学期望 一、离散型随机变量的数学期望 二、连续型随机变量的数学期望 三、数学期望的性质
引例射击问题 设某射击手在同样的条 件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下 命中环数k 0 2 3 4 5 命中次数n 2 13 1510 20 30 频率% 2 1315 10 20 30 n 90 9090 90 90 90 试问:该射手每次射击平均命中靶多少环? 2024年8月27日星期二 目录 上页 下页 返回
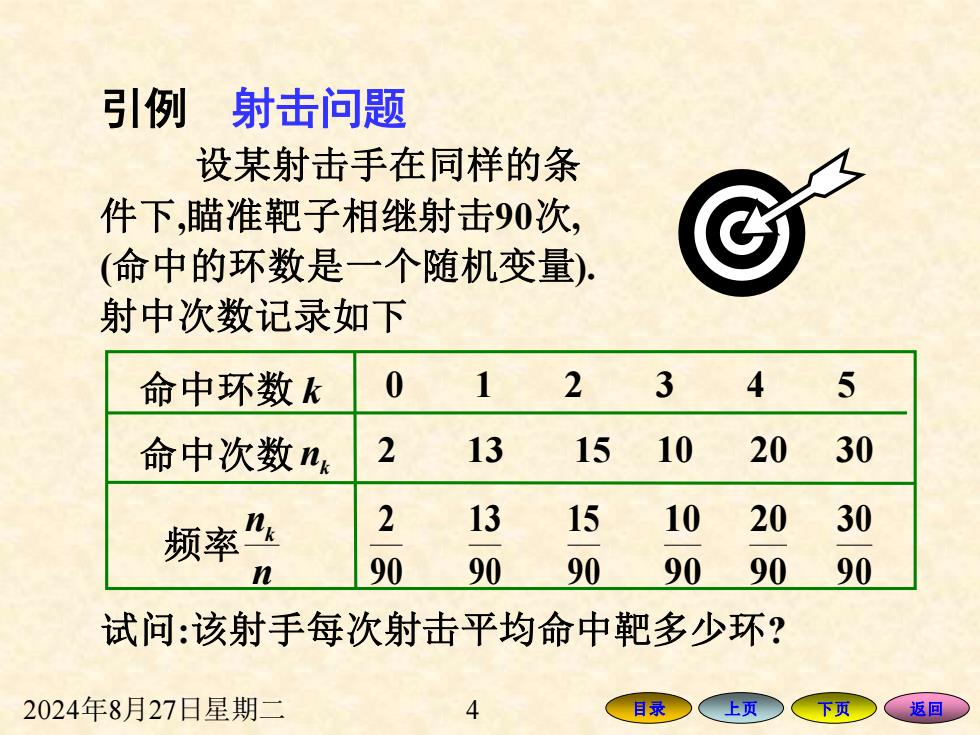
2024年8月27日星期二 4 目录 上页 下页 返回 设某射击手在同样的条 件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下 引例 射击问题 试问:该射手每次射击平均命中靶多少环? 0 1 2 3 4 5 2 13 15 10 20 30 90 15 90 13 90 2 90 20 90 10 90 30 命中环数 k 命中次数 频率 nk n nk

解 平均射中环数= 射中靶的总环数 射击次数 0×2+1×13+2×15+3×10+4×20+5×30 90 2 13 10 20 =0× +1× 15 +2× +3× +4× 90 90 90 90 90 30 +5x 90 k. =3.37. k=0 n 设射手命中的环数为随机变量Y. 2024年8月27日星期二 目录 上页> 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 解 平均射中环数 射击次数 射中靶的总环数 = 90 0 2 + 113 + 215 + 310 + 4 20 + 5 30 = 90 30 5 90 20 4 90 10 3 90 15 2 90 13 1 90 2 0 + = + + + + = 3.37. = = 5 k 0 k n n k 设射手命中的环数为随机变量 Y

平均射中环数 k=0 n 随机波动 频率随机波动 “平均射中环数”的稳定值? n→o ∑kPg k=0 k= 随机波动 稳定值 “平均射中环数”等于 射中环数的可能值与其概率之积的累加 2024年8月27日星期二 6 目录○ 上页 下页 返回
2024年8月27日星期二 6 目录 上页 下页 返回 = = 5 k 0 k n n 平均射中环数 k 频率随机波动 随机波动 = 5 k 0 k n n k n → = 5 k 0 k pk 随机波动 稳定值 “平均射中环数”的稳定值 = ? “平均射中环数”等于 射中环数的可能值与其概率之积的累加