
多雅随机变量及其分市 定义:设随机试验的样本空间为2={ω}: X1(o),X2(o),.,Xn(o)是定义在样本空间2上的随机变量, 则称(X,X2,X)为一个n维随机向量.亦称n维随机变量. n维随机变量(X1,X2,.,Xn)的分布函数定义为: F(x,x2,.xn)=P{X1≤x,X2≤x2,.,Xn≤xn} 上式也称为随机变量X1,X2,.,Xn的联合分布函数。 2024年8月27日星期二 1 目录○ 、上页 下页 返回
2024年8月27日星期二 1 目录 上页 下页 返回 多维随机变量及其分布 定义:设随机试验的样本空间为Ω={ω}. 是定义在样本空间Ω上的随机变量, 则称 为一个n维随机向量.亦称n维随机变量. 1 2 ( ), ( ), , ( ) X X X n 1 2 ( , , , ) X X Xn F x x x P X x X x X x ( , , ) , , , 1 2 1 1 2 2 n n n = n维随机变量 ( , , , ) X X X 1 2 n 的分布函数定义为: 上式也称为随机变量 X X X 1 2 , , , n 的联合分布函数
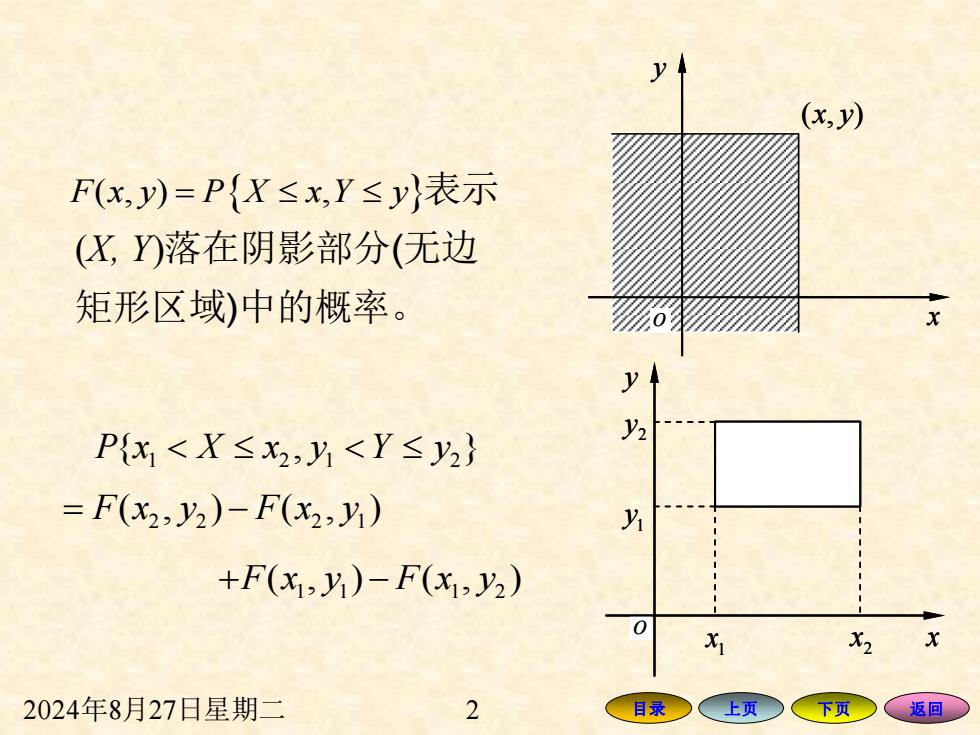
(x,y) F(x,y)=P{X≤x,Y≤y}表示 (X,)落在阴影部分(无边 矩形区域)中的概率。 y P{x<X≤x2,y<Y≤2} y2 =F(x2,2)-F(x2,y) +F(x,y)-F(x1,2) X X2 x 2024年8月27日星期二 2 目录 上页 下页 返回
2024年8月27日星期二 2 目录 上页 下页 返回 F x y P X x Y y ( , ) , = y o x ( , ) x y y o x ( , ) x y 表示 (X, Y)落在阴影部分(无边 矩形区域)中的概率。 y o 2 x 2 y 1 y 1 x x y o 2 x 2 y 1 y 1 x x 1 2 1 2 P x X x y Y y { , } 2 2 2 1 = − F x y F x y ( , ) ( , ) 1 1 1 2 + − F x y F x y ( , ) ( , )

分布函数的性质: (I).Fx,y)分别关于x,y单调非降。 (2).Fx,y)分别关于x,y右连续。 (3).0≤Fx,y)1。 (4).F(-oy)=lim F(x,y)=0 F()=lim F()=0 F(-co,-oo)=lim F(x,y)=0 r-d y-→-00 F(+o0,+o)=lim F(x,y)=1 y→+o0 2024年8月27日星期二 3 目录○ 、上页 下页 、返回
2024年8月27日星期二 3 目录 上页 下页 返回 分布函数的性质: (1). F(x,y)分别关于x,y单调非降。 (2). F(x,y)分别关于x,y右连续。 (3). 0≤F(x,y)≤1。 (4). ( , lim , 0 ) ( ) →− − = = x F y F x y ( , lim , 0 ) ( ) →− − = = y F x F x y ( , lim , 0 ) ( ) →− →− − − = = x y F F x y ( , lim , 1 ) ( ) →+ →+ + + = = x y F F x y

边缘分布 由二维随机变量(X,)的分布函数Fx,y),可以得到它的 两个分量X和Y的分布函数为 Fx(x)=P{X≤x=P{X≤x,Y≤+∞}=F(x,+o) F(y)=P{Y≤y}=P{X≤+oo,Y≤yF(+o,y) 分布函数F(x)和Fy)分别称为二维随机变量(X,Y)关于 X和Y的边缘分布。 2024年8月27日星期二 4 目录 (上页下页 返回
2024年8月27日星期二 4 目录 上页 下页 返回 边缘分布 由二维随机变量(X, Y)的分布函数F(x,y),可以得到它的 两个分量X和Y的分布函数为 F x X ( ) = P X x= + P X x Y , = + F x( , ) F y Y ( ) = P Y y= + P X Y y , = + F y ( , ) 分布函数FX (x)和FY (y)分别称为二维随机变量(X, Y)关于 X和Y的边缘分布

二维离散型随机变量 定义:如果二维随机变量(X,)的所有可能取值是有 限对或可数无限对,则称(X,)是二维离散型随机变量。 P(X=x,Y=yj)=Pi, X y y2 y i,j=1,2,. X P11 P12 pu 称此表为二维离散型 X2 P21 P22 P2j 随机变量(X,)的分布 律,或称为随机变量X Pa P12 Pi 和Y的联合分布律。 2024年8月27日星期二 5 目录 上页 下页 返回
2024年8月27日星期二 5 目录 上页 下页 返回 二维离散型随机变量 定义:如果二维随机变量(X, Y)的所有可能取值是有 限对或可数无限对,则称(X, Y)是二维离散型随机变量。 1 2 1 11 12 1 2 21 22 2 1 2 . . . . . . . . . . . . . . . . . . . . j j j i i i ij y y y x p p p x p p p x p p p X Y P X x Y y p ( , ) , = = = i j ij i j , 1,2, = 称此表为二维离散型 随机变量(X, Y)的分布 律,或称为随机变量X 和Y的联合分布律