三、定积分的几何意义 (3)在区间[a,b],fx)既取正值又取负值时,函数fx)的图形既有在x轴上方的 又有在x轴下方的,此时∫fx)d表示x轴上方的面积减去x轴下方的面积 fe)dc=-4+A,-4: y=f(x) A b B
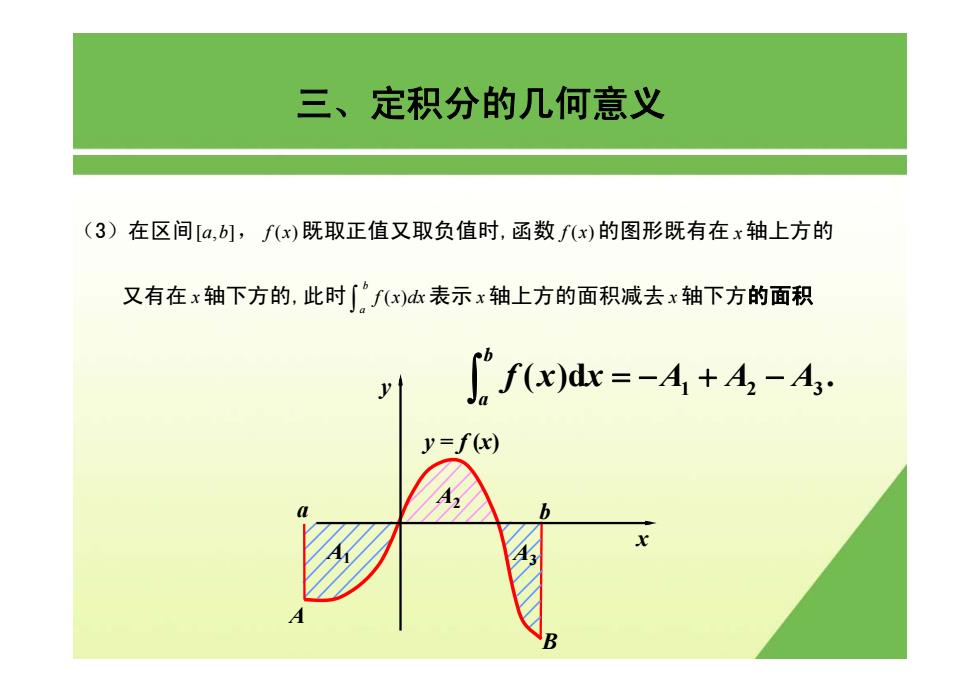
三、定积分的几何意义 (3)在区间[,] a b , f ( ) x 既取正值又取负值时,函数 f ( ) x 的图形既有在 x 轴上方的 又有在 x 轴下方的,此时 ( ) b a f x dx ∫ 表示 x 轴上方的面积减去 x 轴下方的面积 ( ) d . x x A 1 A 2 A 3 f b a = − + − ∫ y = f (x ) A B a b A 1 A 2 A 3 y x

三、定积分的几何意义 例1:求(1)V4-x (2) sin xdx 2 2 2 解: (1)由几何意义4-子达×2=2 (2)由几何意义sinxdx=0
三、定积分的几何意义 例 1 :求(1) 2 2 2 4 x dx − − ∫ (2) sin xdx π ∫−π 解:(1)由几何意义 2 2 2 2 1 4 22 2 x dx π π − − = ×= ∫ (2)由几何意义 sin 0 xdx π −π = ∫

四、可积的条件 定理1:若函数f(x)在[a,b]上连续 定理2:若函数fx)在[a,b1上有界, 则fx)在[a,b]上可积. 且只有有限个间断点, 推论:初等函数在定义区间上可积 则f(x)在[a,b1上可积
四、可积的条件 定理 1:若函数 f ( ) x 在[,] a b 上连续 则 f ( ) x 在[,] a b 上可积. 定理 2:若函数 f ( ) x 在[,] a b 上有界, 且只有有限个间断点, 则 f ( ) x 在[,] a b 上可积. 推论:初等函数在定义区间上可积

五、定积分的性质 规定: ∫fx=0 es=e达 性质1: 「fa)±g(axdr=∫fex)d±∫gx)d 性质2: 心kf)=f)dr(k为常数) 性质3:(定积分的区间可加性)∫fax)dr=∫后fx)dr+∫fx)dr 性质4: 01=6-a
五、定积分的性质 规 定: () 0 a a f x dx = ∫ () () a b b a f x dx f x dx =− ∫ ∫ 性质 1: [ ( ) ( )]d ( )d ( )d b bb a aa f x gx x f x x gx x ±= ± ∫ ∫∫ 性质 2: ( )d ( )d b b a a k f xxk = f x x ∫ ∫ ( k 为常数) 性质 3:(定积分的区间可加性) ( )d ( )d ( )d b cb a ac f x x fx x fx x = + ∫∫∫ 性质 4: 1 b a ⋅ dx b a = − ∫

五、定积分的性质 性质5:(定积分的保号性) 推论1(定积分的单调性) 若在a,1上若fx)≤g(),则 若在闭区间[a,b1上f(x)≥0,则 ∫fa)dr≤∫g)d. d0 推论2 「fxas∫ux (a<b)
五、定积分的性质 性质 5:(定积分的保号性) 若在闭区间[,] a b 上 f x( ) 0, ≥ 则 ( )d 0. b a fx x ≥ ∫ 推论 1(定积分的单调性) 若在[,] a b 上若 f ( ) ( ), x gx ≤ 则 ( )d ( )d b b a a f x x ≤ g x x ∫ ∫ . 推论 2 () () b b a a f x dx ≤ f x dx ∫ ∫ (a b < )