
定理(收敛定理,狄利克雷(Dirichlet)充分条件) 设f(x)是周期为2π的周期函数,并满足条件 1)在一个周期内连续或只有有限个第一类间断点; 2)在一个周期内只有有限个极值点, 则fx)的傅里叶级数收敛,且有 ()当x是fx)的连续点时,级数收敛于fx), (2)当x是fx)的间断点时,级数收敛于 f(x+)+f(x) 注意:函数展成 傅里叶级数的条 2 件比展成幂级数 的条件低得多
定理 (收敛定理,狄利克雷( Dirichlet )充分条件) 设 f (x) 是周期为2的周期函数,并满足条件 1) 在一个周期内连续或只有有限个第一类间断点; 2) 在一个周期内只有有限个极值点, 则 f (x) 的傅里叶级数收敛 , 且有 ( ) ( ) , 2 f x f x 注意: 函数展成 傅里叶级数的条 件比展成幂级数 的条件低得多. (1) 当x是f(x)的连续点时,级数收敛于f(x). (2) 当x是f(x)的间断点时,级数收敛于

例1以2π为周期的矩形脉冲的波形 0≤x<π ,-π≤x<0 将f(x)展开成傅里叶级数, 解:所给函数满足狄利克雷充分条件 在点x=kπ(k=0,士1,±2,.)处不连续 收敛于1+1
解:所给函数满足狄利克雷充分条件. 在点xkk ( 0, 1, 2, )处不连续 1 1 0, 2 收敛于 1 2 1, 0 ( ) 1, 0 ( ) . x f x x f x 例 以 为周期的矩形脉冲的波形 将 展开成傅里叶级数 o x f x( ) 1 1
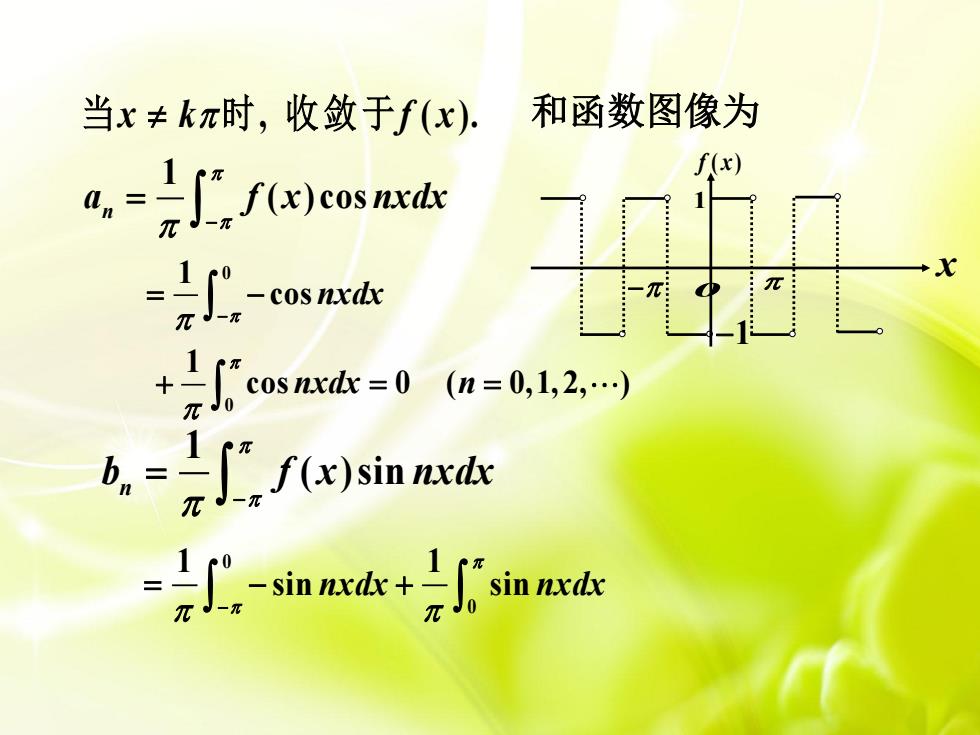
当x≠kπ时,收敛于f(x). 和函数图像为 f(x) a=∫fux)cos nxds -If-cosnxds 了cosm=0n=0,12, bn=∫fx))sinnd =号∫,-sina+君广sind
当x k f x 时, ( ). 收敛于 和函数图像为 1 ( )cos n a f x nxdx 0 0 1 cos 1 cos 0 ( 0,1, 2, ) nxdx nxdx n 1 ( )sin n b f x nxdx 0 0 1 1 sin sin nxdx nxdx o x f x( ) 1 1

1-c0sm)=2I1-(-1y1 nπ nπ 4 n=2k-1,k=1,2,. (2k-1)π 0, n=2k,k=1,2,. 所求函数的傅氏展开式为 4 x)=721-0z sin(2n-1)x (-0<x<+0;x≠0,士π,±2π,)
2 (1 cos ) n n 2 [1 ( 1) ] n n 4 , 2 1, 1, 2, (2 1) 0, 2 , 1, 2, n k k k n k k 1 4 ( ) sin(2 1) (2 1) ( ; 0, , 2 , ) n f x n x n x x 所求函数的傅氏展开式为
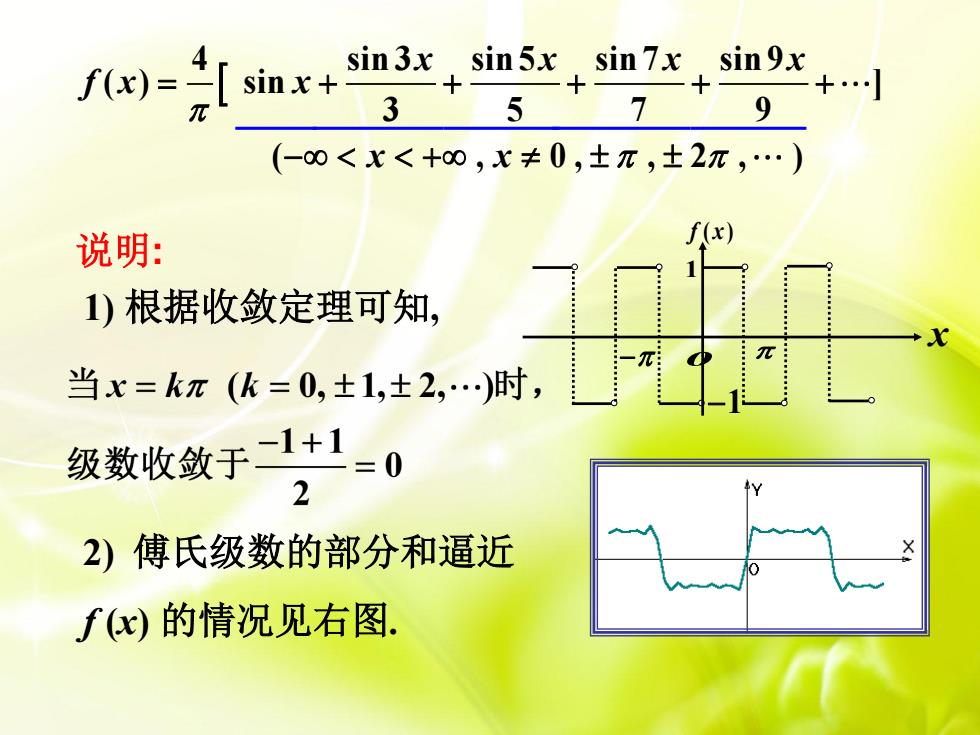
f()= sinx+ sin3x sin5x sin 7x sin9x +.小 3 5 7 9 (-00<X<+0,x≠0,±元,±2π,.) 说明: 8429 1)根据收敛定理可知, ≥0 级数收敛于-1+ 2)傅氏级数的部分和逼近 fx)的情况见右图
1) 根据收敛定理可知, 2) 傅氏级数的部分和逼近 f (x) 的情况见右图. 4 sin 3 sin 5 sin 7 sin 9 ( ) sin ] 3 5 7 9 ( , 0 , , 2 , ) x x x x f x x x x 说明: o x f x( ) 1 1