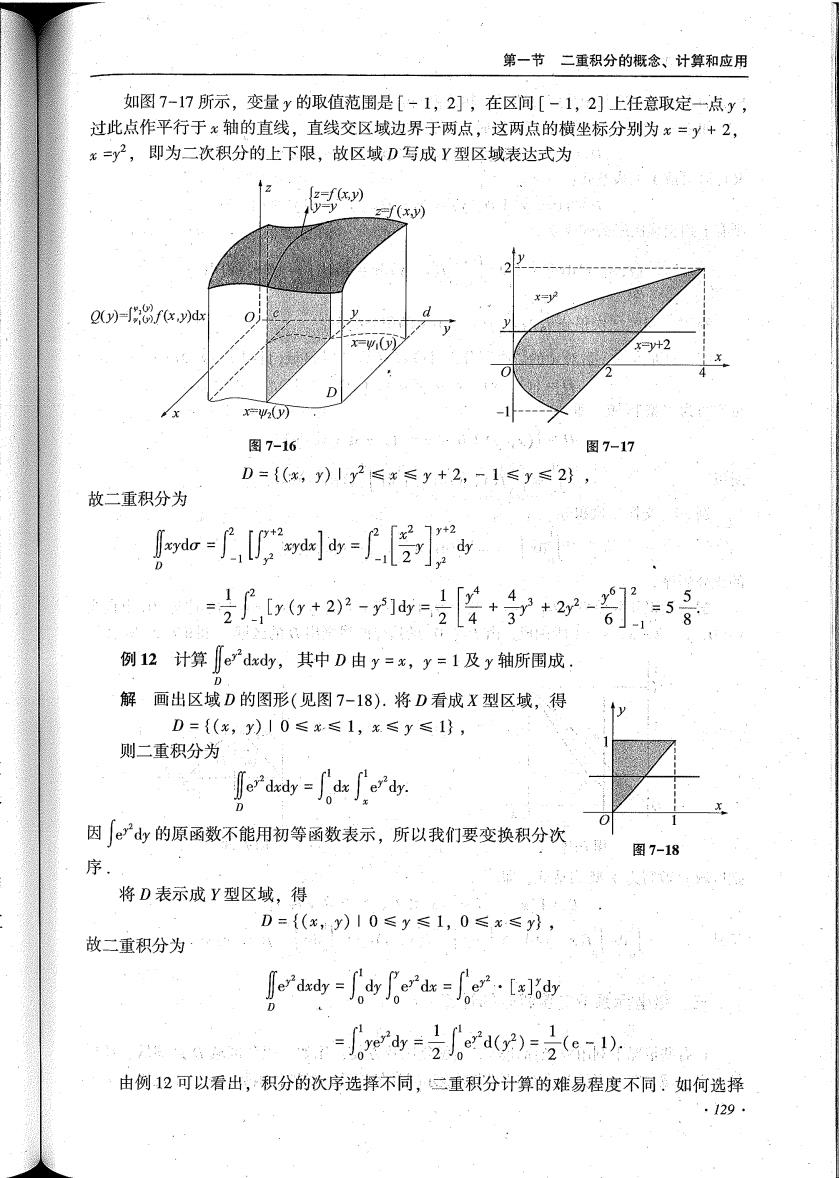
第一节二重积分的概念、计算和应用如图7-17所示,变量的取值范围是[-1,2],在区间[-1,2】上任意取定点y,过此点作平行于轴的直线,直线交区域边界于两点,这两点的横坐标分别为%=y+2,=y,即为二次积分的上下限,故区域D写成Y型区域表达式为2(z-f(x,y)-1f(xy)0()-f(x)dx=y+2)图7-16图7-17D=((%, y) 1 ≤x≤y+2, -1≤y≤2),故二重积分为Jxydo =' [ xyde] dy=" dyV14[(+2)21dy=号36例12计算er"dxdy,其中D由y=%,y=1及y轴所围成,解画出区域D的图形(见图7-18).将D看成X型区域,得D=((x,)/ 0≤x≤1,x≤≤)则二重积分为[er dxdy:Drdy的原函数不能用初等函数表示,所以我们要变换积分次大图7-18序将D表示成Y型区域,得D=((%,)10≤≤1, 0≤故二重积分为Ter'dxdy=edx[x],dy1-yer'dyer'd(r)=2(e71)由例12可以看出,积分的次序选择不同,二重积分计算的难易程度不同,如何选择129

第七章多元函数积分学等禁积分的次序呢?这与积分区域的形状和被积函数的特性有关系。如果一个积分区域D既可以写成X型表达式:D =(x,y)1p(x) ≤y≤p2(x), a≤x≤b),又可以写成Y型表达式:D=t(%, y) I (y) ≤x≤2(y),c≤y≤d),则有下列交换次序公式成立.Jf(x, ) dedy =[" dx ["(a)(f(x, y)dy ='dyf(x,y)dx..例13交换二次积分dx(,y)dy的积分次序,解这是先对y后对的二次积分,对应着D的X型区域(见图7-19)为D=((x, y)1 %2 ≤y≤x,0≤x≤1),可改写为Y型区域,即D=((x,y)10≤≤1,≤x≤/,所以['da J(x, )dy=f'dy 'f(x, y)d例14交换二次积分['da f(x, y)dy+f'de f(a, y)dy的积分顺序解设积分区域D=D,+D2,其中D,由直线y=0,y=%,%1所围成,D2由直线y=0,y=2-%,%=1所围成,由D,、D2的边界曲线画出D的区域,如图7-20所示.yY图7-19图7-20把区域D改写为Y型表达式,即0D={(x,y)l≤x≤2-y,0≤y≤1),于是'dxf(r,)dy+fdafox,y)dy=fdyf(x,y)d三、极坐标系下二重积分的计算在有些情况下利用极坐标计算二重积分比较方便,比如,积分区域D是圆域、环形域、扇形域,即D的边界曲线用极坐标表示时比较简洁;或被积函数(y)用极坐标表.130+

第一节二重积分的概念、计算和应用示时比较简洁,比如V+y,arctan等,均可考虑利用极坐标系计算二重积分r=V?+yx=rcoso直角坐标系与极坐标系的转换公式为成= rsing0:=arct下面我们介绍极坐标系下的二重积分的计算方法AE在直角坐标系下,面积微元do可以写成dxdy,那么在极坐标系下,面积微元怎么表示呢?在极坐标系下,设过极点0的射线与平面闭区域D的边界曲线最1多相交于两点(见图7-21):由图7-21极坐标的定义可知,若极径r=c,c是一个常数,则表示圆心在极点,半径为c的一个圆;若极角=c,c是一个常数则表示一个从极点出发的射线,现以极点为中心作一组同心圆二1,从极点出发作一组射线=の,将区域D分成n个小闭区域,这些区域的面积记为Ao(i=1,2,…,n),除了包含边界点的一些小区域外,o,的面积都可以看作是两个圆扇形的面积之差,因此-1rA0Ag(r+ Ar)2A0,21(Ar)240, rAr,40.=r,Ar,A0,2于是就得到了极坐标系下的面积微元do = rdrdo.若已知直角坐标系下的二重积分门If(*,)d,则用以下方法可以把其变换为极坐标D系下的二重积分,(1)将积分区域D的边界曲线用极坐标方程表示(2)利用变换×=rcoso,y=rsine将被积函数f(,y)转化成r、的函数:f(x, y)=f(rcoso, rsino).(3)将面积微元do转化为极坐标下的面积微元rdrdo:则二重积分的极坐标系下的表达式为Jf(x, y)do - Ji(rcoso, rsino)rdrde.极坐标系下的二重积分,同样是转化为二次积分来计算,我们分三种情况来讨论(1)如果积分区域D介于两条射线=α,=β之间,而对D内任一点(r,e),其极径总是介于曲线=r(0))元=+2(6)之间(见图7-22),则区域D的表达式为1(r, 0)1α≤0≤, (0)≤r≤r2(0)1.于是131

第七章多元函数积分学[(x, y)dxdy = [(rcoso, rsino)rdrdoDcr2(6)def(rcoso,rsino)rdr.具体计算时,内层积分的上、下限可按如下方式确定:从极点出发在区间(α,β)上任意作一条极角为的射线穿透区域D(见图7-22),则进人点与穿出点的极径r(0)、T2(の)就分别为内层积分的下限与上限(2)如果积分区域D是如图7-23所示的曲边扇形,则可以把它看作是第一种情形中当r()=0,r2(0)=r(0)的特例,此时,区域D的表达式为1(r,0) 1α≤0≤β,0≤r≤r(0)1.于是cr(0)[f(x, y) dxdy =def(rcoso,rsino)rdr.HN(3)如果积分区域D如图7-24所示,极点位于D的内部,则可以把它看作是第二种情形中当α=0,β=2π的特例,此时,区域D的表达式为1(r, 0) [0i≤ 0 ≤2,0≤T≤r(0)1于是2(0)r(0)ri(0)7L图7-22图7-23图7-24r(0))dxdyf(rcose,rsino)rdr.YD注根据二重积分的性质4,闭区域D的面积在极坐标系下可表示为rdrdo.do:b如果区域D如图7-23所示,则有rr(0)1rdrde :2(0)do.drdr2.JoO例15将下列区域(见图7-25)用极坐标表达式表示(1) D =((x, y) 1 x2 +y2 ≤2x):(2)D=(,y)1x +y2≤y) ;(3)D=(,y)x+y≤a(a>0));(4)D为y=x,y=0与%=1所围区域解(1)区域D的边界曲线为x2+y2=2x:令x=rcoso,y=rsino,则有表达式=2coso77TT再令r=0,则有cos=0,即0=或0=,从而0的变化范围为22☆7022·132

第二重积分的概念、计算和应用o(2)(3)(4)(1)图7-25从极点出发作条极角为的射线,交区域边界于两点:r=0,r=2coso.故区域的极坐标表达式为"TT(,0)0≤2cs0)三02.2.(2)区域D的边界曲线为2+y2=y.令x=rcoso,y=rsine,则有表达式r=sing再令r=0,则有=0或=,从而的变化范围为0≤0≤T.从极点出发作一条极角为α的射线,交区域边界于两点:r=o,r=sino.故区域的极坐标表达式为((r,0)10≤r≤sino, 0≤≤).(3)极点在区域D的内部,故6的取值范围为0≤≤2π.边界曲线2+y2=a2的极坐标方程为r=a,故区域的极坐标表达式为(,0)10≤r≤a,0≤6≤2m)(4)利用极坐标变换式=rcoso,=rsine可知直线y=×的极坐标方程为=直线%=1的极坐标方程为r故区域D的极坐标表达式为cosAT0≤0coso例16计算e-rdg,其中D是由中心在原点,半径为a的圆周所围成的闭区域,D解在极坐标系下,D={(r,)10≤r≤a,0≤≤2),则e--y'do e-"rdrdo06S= m(l -e-a2)Va3--2-ydy,其中积分e"dy不能注1若用直角坐标系形式,则有1=dVa3e用初等函数表示其结果,因此用无法求原函数的途径解决,注2可以利用本题的结果计算积分1=dr先考虑?=e-x?dx :e*dx=dady其中ed13.3