
第七章多元函数积分学的时候,可以把%看成是常数,故原函数为,因此定积分的值为2x+1(α+y)dy=*.[y] +[y=x(1-0)+号-(12 = 02)= % 这是一个关于的函数,例5计算二重积分Jerdxdy,其中区域D是由=0,=1,=0,y=1所围成的D矩形.解因为D是矩形区域,且e+y=e*·e,所以Jer+rdrdy=f'da 'e*erdy =f'e'deydf'e"[e'Jde-f'e(e- 1)da =(e - 1)?我们还可以通过另一个截面来求曲顶柱体的体积,从而得到二重积分的另一个计算方法现过y轴上任一点yo做垂直于y轴的截面,得到一个以[α,b]为底、以曲面z=f(x,y)和平面y=yo的交线y=f(%,yo)为顶的曲边梯形(见图7-9),其面积为Q(yo)Yo)dxz-f(xy)-12=f(x,y)0-(x.y.)d0图7-9由yo的任意性可知,过轴上任一点的截面面积为Q(y)=(x,y)d,这是的函数利用已知截面面积的立体体积公式可知,曲顶柱体的体积是V=,o(n)dy-'['(, )da] dy(2)式(2)的右端称为先对x、后对y的二次积分,上述公式也记为V='["'(r, y)da] dy=f'dy J'f(x, y)dx·124

第一节二重积分的概念、计算和应用因此我们可以得到矩形区域上的二重积分的计算公式:(x, y)ddy =J'da J'f(x, y)dy =dyf(x, y)dx.D-[a, b]x[c, d]上式对f(%,)<0也成立例5也可以用另外一种次序的二次积分来计算,Je*rdxdy - I'dy f'ee' de - ferdye*df'e'[e*,dy -f'e(e - 1)dy =(e - 1)2.例6计算1=xy2dxdy,其中D=[0,1]×[1,2].1解f(,y)=xy2在D上连续,若先对积分后对积分,则有1-Jopdady=oda-fr[] ay-pay-[]--若先对积分后对积分,则有I upddy -fan umpdy []'d ad []2.X型区域上的二重积分若积分区域D可以用不等式((x,y)1 pi()≤y≤p2();a≤x≤b)来表示(见图7-10),其中函数Φ()、2(x)在区间【a,b】上连续,这样的区域称为X型区域,其区域特征为:穿过D内部且平行于轴的直线与D的边界最多相交于两点,yty=p2(x)yty=p2(x)y=g(x)y=pi(x).1aa(b)图7-10例7将下列区域(见图7-11)写成X型区域的表达式b:解(1)三角形斜边的方程为y=故区域的X型表达式为b0一%,0≤x(2)抛物线的方程为=x2,直线的方程为y=%,故区域的X型表达式为((x,)1x≤y≤x,0≤x≤)(3)上半圆的方程为y=/1-x,下半圆的方程为y=-/1-x,故区域的X型表125
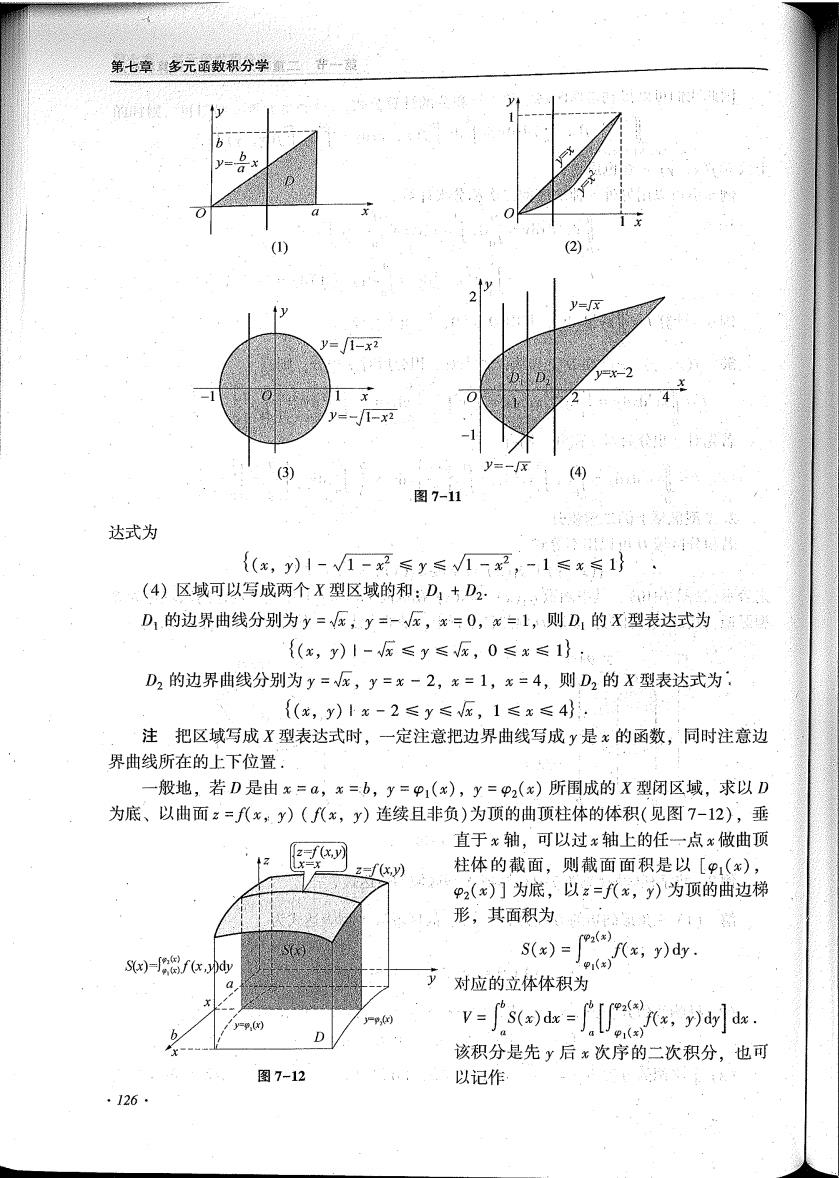
第七章多元数积分学(1)/1-x2-Jx(3)4图7-11达式为((x,y)1-V1-x≤y≤/-,-1≤x≤1)(4)区域可以写成两个X型区域的和:D+D2.D,的边界曲线分别为y=,y=-x,x=0,α=1,则D,的X型表达式为((, ) 1-/x≤≤/x, 0≤x≤1)D,的边界曲线分别为=Vx,=-2,%=1,%=4,则D,的X型表达式为((x, )1-2≤≤x, 1≤x≤4)注把区域写成X型表达式时,一定注意把边界曲线写成是α的函数,同时注意边界曲线所在的上下位置:般地,若D是由=a,=b,=(x),=2()所围成的X型闭区域,求以D为底、以曲面z=f(,y)((,)连续且非负)为顶的曲顶柱体的体积(见图7-12),垂直于×轴,可以过轴上的任一点做曲顶[z=f(x,y)柱体的截面,则截面面积是以【(),f(x,y)p2()为底,以z=(x,)为顶的曲边梯形,其面积为、S(x)=f(x, y)dy.S(x)-fea)f(xjd)V.对应的立体体积为2('s(x)dx = /V-f(x, y)dy](x该积分是先后次序的二次积分,也可图7-12以记作·126

第一节二重积分的概念、计算和应用92()f(x, y)dy.从而[(x, )ddy ='s(a)dx =,[(x, )dy] dx =daf(x, y)dy.(3)式(3)表明,将二重积分转化为先后次序的二次积分来计算,关键是确定二次积分中关于变量y的积分限,即确定区域D的X型表达式:如果区域是如图7-12所示的X型区域,在区域[a,b]上任意取定一点,并过此点做一条平行于轴的直线,顺着轴正向的方向看去,直线与边界曲线的第一个交点的纵坐标()就是积分的下限,第二个交点的纵坐标2()是积分的上限,这个关于变量的积分计算的结果是的函数,再对变量在区间【a,b]上做定积分即可,式(3)对f(,y)0也成立例8计算二次积分dxydy.解设S(x)=xydy,被积函数是关于、y的二元函数,积分变量是,则可以把%看成常数,被积函数的原函数为%y,则23[]--s(x) =x :~2于是 da Jexdy =,S(a) da=→,( -) da1a4+[(-g) (()]1014724注在计算第一个定积分xydy时,y是自变量,看成常数;而计算第二个定积分(3-x2)dx时,是积分变量,例9计算[xydo,其中D是由直线=1,=2及=所围成的闭区域D解如图7-13所示,把区域写成X型表达式,则有D=(x,)11≤≤x,1≤x≤2),所以[Jopda-U ] d - [号] d-(6-)[8--8例10计算/1+2-do,其中D是由直线=%,x=-1和y=1所围成的闭区域.解如图7-14所示,把D写成X型表达式,即D=(x,y)lx≤y≤l,-1≤x,127

第七章多元函数积分学图7-1图7-则y?dg:y+x?-yd[1+-)'d(1 ×/3 - 1)dx = -1)d23.Y型区域上的二重积分设积分区域D可以用不等式((x,y)l(y)≤x≤2(y),c≤y≤d)来表示(见图7-15),其中函数(y)、中2(y)在区间[c,d】上连续,这样的区域称为Y型区域,穿过D内部且平行于轴的直线与D的边界最多相交于两点ytax=Wi(y)x=yi(y)x=w2(y)x-W(y)x.o图7-15若D是由y=c,y=d,=(y),x=2(y)所围成的Y型区域,类似于X型区域上的曲顶柱体所围体积求法,以D为积分区域,以二元函数z=f(,2)为被各函数的二重积分的值等于一个先对后对的二次积分(见图7-16),即'ody='[a, da] dIf(x, y) dxdy = Jf(x,y)dx(例11计算二重积分xyda,其中D是由抛物线y2=及直线y=%~2所围成的闭区域,解首先求抛物线y?=%及直线y=%-2的交点,即解方程组%=x-2,解得交点坐标为(1,1)和(4,2)·128