
所以在每个向量前面添加r个分量而得到的n-1个n维向量x,x,,/4,也是线性无关其次,证明齐次线性方程组的任一解él.e4e3élix=eelr+1ué /ue3élna可由x,x,,4,x,线性表示.加油!

作向量h=1 +x,+1 +22+/+1,n-由于51,52.,5n-r是齐次线性方程组的解,故m也是齐次线性方程组的解比较h和x,它们后边n-r个分量对应相等,而线性方程组(3)表明它的任一解的前r个分量可由后n-r个分量唯一确定,因此h=x,即X =1 r+, +1 r+2X2 +/4 +1 ,Xn-r因此x,x,,,xn-,是解空间的一个基,从而知解空间的维数为n-r加油!

注意:1.当 R(A)=r< n 时,方程组 Ax=0 有无穷解当R(A)=n 时,方程组 Ax=0 只有零解2.方程组的基础解系不唯一方程组Axr=0的任意n-r个线性无关的解向量都可以作为基础解系加油!
2.方程组的基础解系不唯一 方程组 的任意n-r个线性无关的解向量, 都可以作为基础解系. 1.当 R(A)=r < n 时,方程组 有无穷解, 当 R(A)=n 时,方程组 只有零解. 注意:
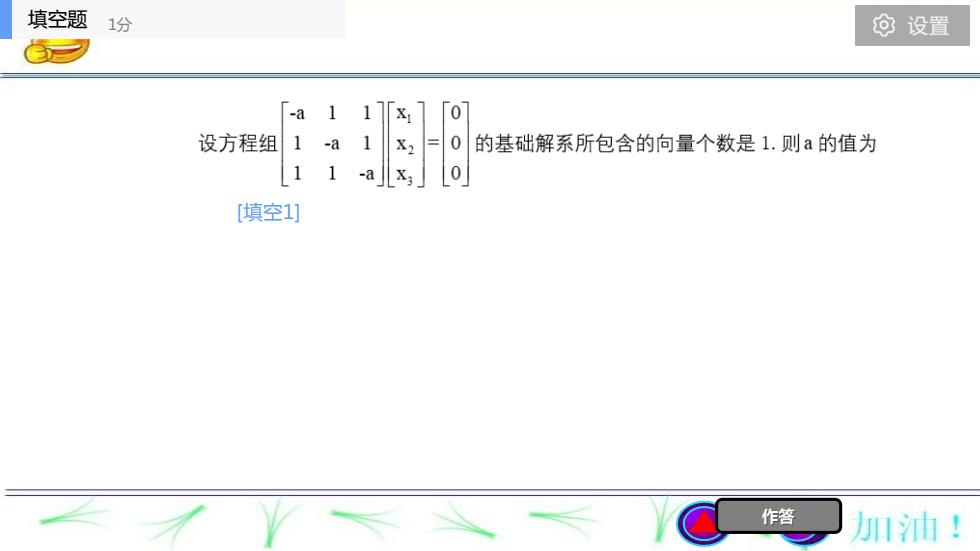
填空题1分设置-a1设方程组1-a的基础解系所包含的向量个数是1.则a的值为11[填空1]作答加油!
[填空1] 作答 填空题 1分

设1,2,.,sn-r是方程组Ax=0的一个基础解系,则方程组的任一解可表示为x=kx, +k,x, +/ +kn-rxn-r上式称为齐次线性方程组的通解解空间可以表示为加油!
设ξ1 , ξ2 , .,ξn-r是方程组 的一个基础解系, 则方程组的任一解可表示为 上式称为齐次线性方程组的通解 解空间可以表示为