
定理1 设R(A)=r< n,则AX=0有基础解系,且所含向量个数为n-r,即dimW=n-r,这里n为方程组未知数个数证:设齐次线性方程组系数矩阵A的秩为r.不妨假设A的前r个列向量线性无关,于是A的行最简形为0/sélbr+1/4bi,ie//sV/4/4eoVA1br-1VAbtB ==a/00/4-6ei/s///4/<二00VsV4:000加油!
定理1 设R(A) = r < n, 则AX = 0有基础解系, 且所含向量个数为n - r, 即dimW = n - r, 这里n为方程组未知数个数. 证: 设齐次线性方程组系数矩阵A的秩为r,不妨假 设A的前r个列向量线性无关,于是A的行最简形为

与B对应的线性方程组为ix=-bir+x++ - /4- b.,x.12/4/4(3)=- br++ - /4- b,X,x我们把x+1x,称为自由未知量加油!
与B对应的线性方程组为 我们把xr+1,.,xn称为自由未知量
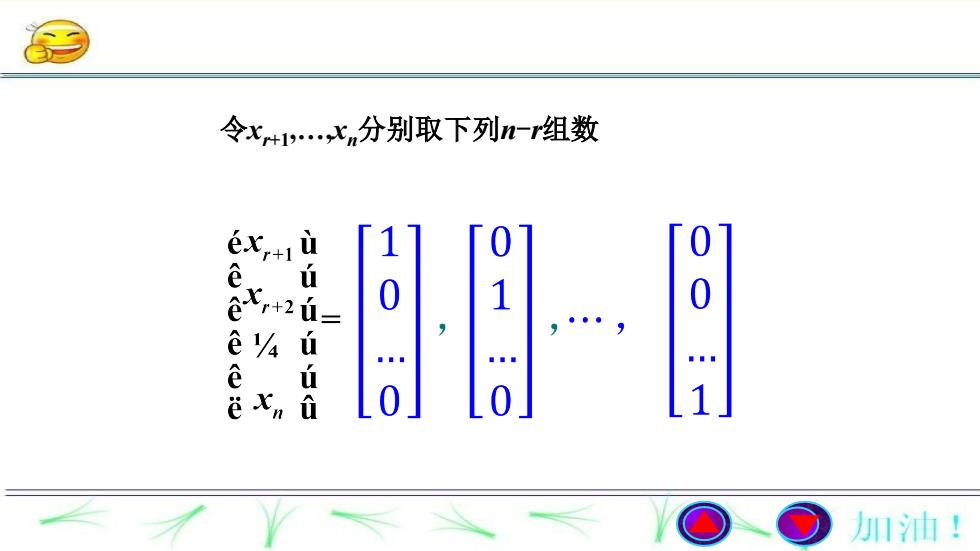
令xr+1...x,分别取下列n-r组数000中ex1<eu001otXr+2e /uéu0福Xn1é加油!
令xr+1,.,xn分别取下列n-r组数

二代入(3)中依次可得uué- b,ué- b.é-b.éx,u21,neUe<eCTu4/41/4e<eu'ueie- b,.心b21iubb@x,ir,r+1urnu从而得到齐次线性方程组的n-r个解seeeeeceeeba.né- b,+2 ié- bir+rucd888888baad0A/Vbb2F+eeeeeevanu<0001X, =-X,e=0ee01/4/4ee001C加油!
代入(3)中依次可得 . 从而得到齐次线性方程组的n-r个解

下面证明x,,x,,/4,x.是解空间的一组基éx+uéu北0Cr+2u所取的n-r个n-r维向量首先由于é /u<euéXnaéououé1ueee<eu<euoUA0e<eui.Li-线性无关e/ ie/ u'e/eeeeUue001加油!