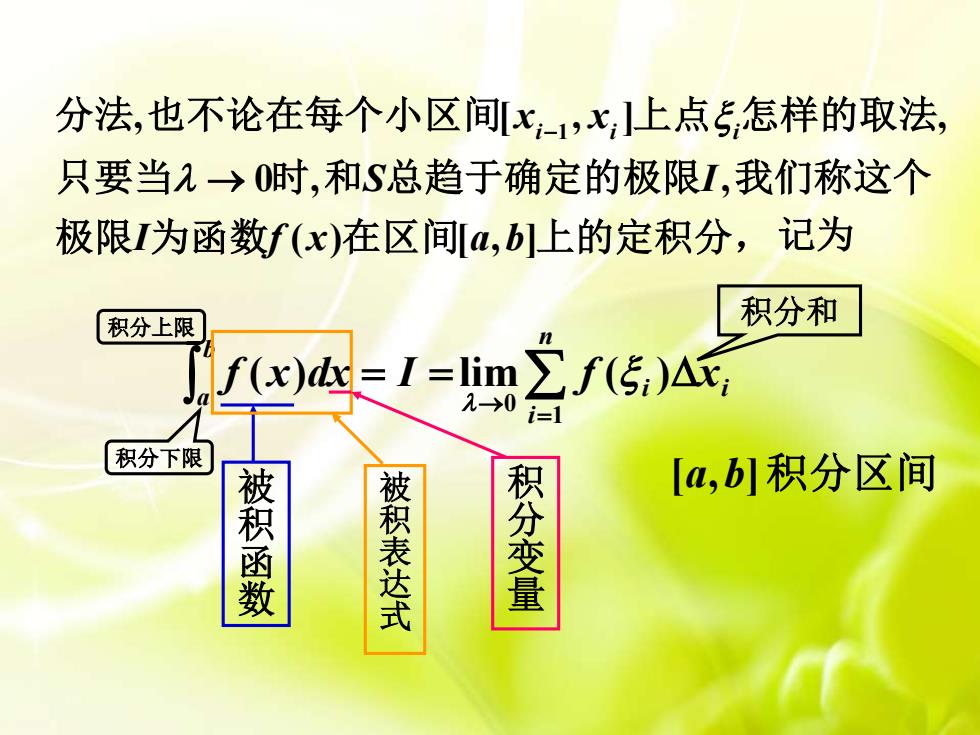
分法,也不论在每个小区间[x;-1,x,]上点5,怎样的取法只要当→0时,和S总趋于确定的极限I.我们称这个极限I为函数f(x)在区间[a,b]上的定积分,记为积分和积分上限nZf(5)Ar,f(x)dx= I =lim2-0i=1积分下限[a,b]积分区间积分变量被积函数被积表达式
= = ba f (x)dx I i i ni f x = → lim ( ) 1 0 被积函数 被积表达式 积分变量 [ , ] a b 积分区间 记为 积分上限 积分下限 积分和 1 , [ , ] , 0 , , ( ) [ , ] i i i x x S I I f x a b − → 分法 也不论在每个小区间 上点 怎样的取法 只要当 时 和 总趋于确定的极限 我们称这个 极限 为函数 在区间 上的定积分,

n2[° J(x) dx =lim(5)Ax;2-0i-1定积分实质上就是无穷多个无穷小量的和,它体现了一种无限细分、无限求和的思想。化整为零积零为整
定积分实质上就是无穷多个无穷小量 的和,它体现了一种无限细分、无限求 和的思想。 化整为零 积零为整 ( ) ( ) 0 1 → = = lim n b i i a i f x dx f x

>注意:(1)定义中区间的分法和,的取法必须是任意的;(2)定积分的值是个数,积分值仅与被积函数及积分区间有关,而与积分变量的记法无关f'f(x)dx =f'f(t)dt = f'f(u)du(3)当函数f(x)在区间[a,bl上的定积分存在时称函数f(x)在区间[a,b上可积
➢注意: b a f (x)dx = b a f (t)dt = b a f (u)du (2)定积分的值是个数,积分值仅与被积函数 及积分区间有关,而与积分变量的记法无关. (1) i 定义中区间的分法和ξ 的取法必须是任意的; (3) ( ) [ , ] ( ) [ , ] . f x a b f x a b 当函数 在区间 上的定积分存在时, 称函数 在区间 上可积

定积分存在定理定理1设函数f(x)在区间[a,bl上连续则函数f(x)在区间[a,b]上可积设函数f(x)在区间[a,b]上有界,且只有有限定理2个间断点,则函数f(x)在区间[a,b|上可积
定理1 定理2 定积分存在定理 ( ) [ , ] , ( ) [ , ] . f x a b f x a b 设函数 在区间 上连续 则函数 在区间 上可积 ( ) [ , ] , , ( ) [ , ] . f x a b f x a b 设函数 在区间 上有界 且只有 限 个间断点 则函数 在区间 上可积

x'dx.例1利用定义计算定积分S解 将[0,1]n等分,分点为x; =一,(i=1,2,,n)M小区间[x;-1,x,]的长度△x;=二,(i=1,2,..",n)n取5, = x, (i= 1,2,...,n)Zf(5)Ax; -2 5Ax, =Zx;Ax,i=1i1i=-1
例1 利用定义计算定积分 . 1 0 2 x dx 解 将[0,1]n等分,分点为 n i xi = ,(i = 1,2,,n) 小区间[ , ] i 1 i x x − 的长度 n xi 1 = ,(i = 1,2,,n) 取 i i = x ,(i = 1,2, ,n) i i n i f x = ( ) 1 i i n i = x = 2 1 , 1 2 i n i i = x x =