
设g在[0,a]上连续,f二阶可导,且f"(α)≥0,证明课前练习:Fa(t)dtf(s(t)dt ≥f/ /【2018年第十届全国初赛非数学类】六(14分)证明:设连续函数f(α)>0,有In ff(a)da ≥ f'lnf(a)d c

讲座开始前练习参考解答课前练习:设在[0,al上连续,f二阶可导,且f"α)≥0,证明:J"f(t)dt ≥ ↑(, J"s(t)dt)aakak【参考证明]:设T为[0,a]的n份均分割,则分点为,k=0,1,.",n,即ak由nnf"(α)≥0知f是凸函数(凹曲线),故由琴声(Jesen)不等式中,令入=二,则n(()(s(a)即(a)((a)%由于f,在[0,a]上都可积,且f连续,故在上式中令n→8,得()dt≤"[(t)dt
讲座开始前练习参考解答

第5讲一元函数积分学及其应用李海玲山东理工大学
第5讲 一元函数积分学及其应用 山东理工大学 李海玲

不定积分计算的一般思路三定积分的概念、性质及其应用变限积分函数的性质及相关问题求解四定积分计算的一般思路二五定积分常见几何应用与物理应用六、反常积分及其敛散性的判定
l 一、不定积分计算的一般思路 l 二、定积分的概念、性质及其应用 l 三、变限积分函数的性质及相关问题求解 l 四、定积分计算的一般思路 l 五、定积分常见几何应用与物理应用 l 六、反常积分及其敛散性的判定
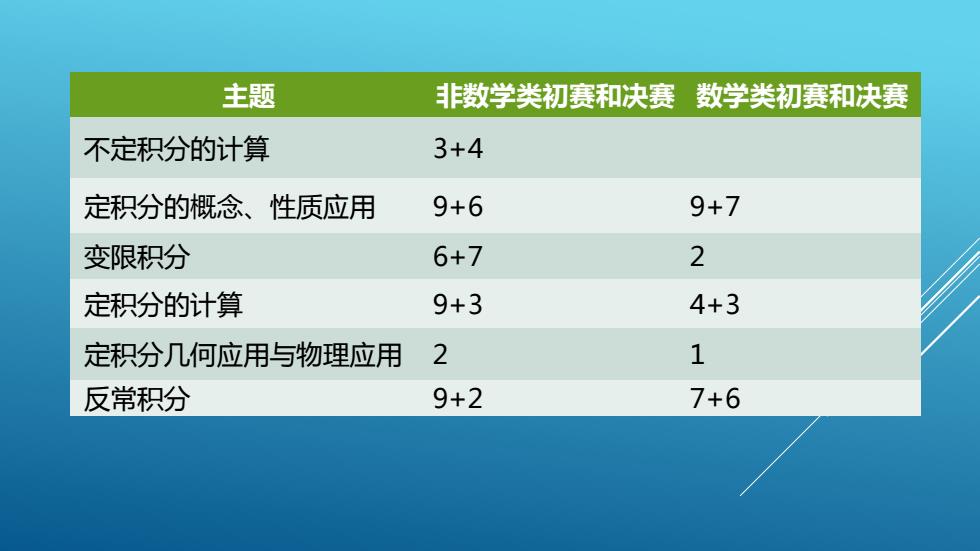
主题非数学类初赛和决赛数学类初赛和决赛3+4不定积分的计算9+69+7定积分的概念、性质应用26+7变限积分9+34+3定积分的计算12定积分几何应用与物理应用9+27+6反常积分
主题 非数学类初赛和决赛 数学类初赛和决赛 不定积分的计算 3+4 定积分的概念、性质应用 9+6 9+7 变限积分 6+7 2 定积分的计算 9+3 4+3 定积分几何应用与物理应用 2 1 反常积分 9+2 7+6