(1)曲边梯形如图所示,在区间[a,b内任意插入若干个分点a=x,<x, <x,< <xn-1<x,=b把区间[a,b]分成nJ个小区间[xi-1,x;],长度为△Ar;Ax, = X; - Xi-1 'olaxXi-1 X, x-,bi=1,2,.,n;这样,把曲边梯形分割为n个窄曲边梯形:
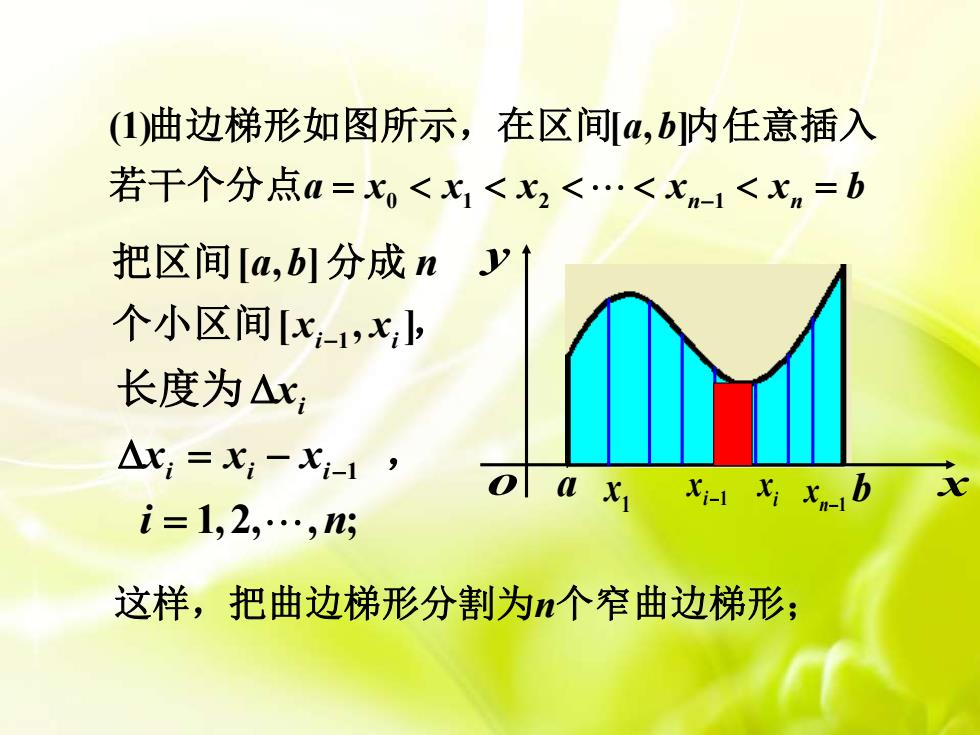
1 [ , ] [ , ] i i a b n x x − 把区间 分成 个小区间 , a b x yo i x 1 x i 1 x − n 1 x − 这样,把曲边梯形分割为n个窄曲边梯形; 1 1,2, , ; i i i i x x x x i n − = − = 长度为 , 0 1 2 1 (1) [ , ] n n a b a x x x x x b = = − 曲边梯形如图所示,在区间 内任意插入 若干个分点

(2)在每个小区间[x;-1,x;]上任取一点,以[xi-1,x;为底,f()为高的小矩形的面积近似窄曲边梯形的面积,则A, ~ f(E)Ax, i = 1,2,..,n(3)曲边梯形面积的近似值为ZAA, ~E f(5,)Ar;A=olbaXXn-1Xi-1i-1(4)当分割无限加细时,设所有小区间长度的最大值=max[△xj,△x2,…Ax,},当→0时,Zf(5)Ax;曲边梯形面积为 A=lim1-0i=1
1 1 ( ) n n i i i i i A A f ξ x = = = (3)曲边梯形面积的近似值为 1 2 (4) , max{ , , } 0 n λ = → x x x λ 当分割无限加细时 设所有小区间长度的 最大值 ,当 时, i n i i A = f x = → lim ( ) 1 0 曲边梯形面积为 1 (2) [ , ] i i i x x ξ 在每个小区间 − 上任取一点 , ( ) 1,2, , A f i i i = ξ x i n 1 [ , ] ( ) i i i x x f ξ 以 − 为底, 为高的小矩形的 面积近似窄曲边梯形的面积,则 a b y o i x 1 x i 1 x − n 1 x − i

实例2(求变速直线运动的路程)设某物体作直线运动,已知速度v=v(t)是时间间隔[T,T]上t的一个连续函数,且v(t)≥0,求物体在这段时间内所经过的路程思路:以不变代变 把整段时间分割成若干小段,每小段上速度看作不变,求出各小段的路程再相加,便得到路程的近似值,最后通过对时间的无限细分过程求得路程的精确值
实例2 (求变速直线运动的路程) 设某物体作直线运动,已知速度v = v(t)是 时间间隔[ , ] T1 T2 上 t 的一个连续函数,且 v(t) 0,求物体在这段时间内所经过的路程. 思路:以不变代变 把整段时间分割成若干小段, 每小段上速度看作不变,求出各小段的路程再 相加,便得到路程的近似值,最后通过对时间 的无限细分过程求得路程的精确值.

T=t <ti<t,<...<tn-i<tn =T(1)分割At, = t; -ti-1(2)近似4S, ~v(t,)At, i =1,2,..,n则 S~Zv(t,)At;(3)求和i=1(4)取极限a = max[Ati,At2,...,△tn}2路程的精确值v(T,)At;S=lim1-0i-l
(1)分割 1 0 1 2 1 T2 T t t t t t = n− n = i = i − i−1 t t t ( ) 1,2, , (2)近似 S v t i n i i i = 1 ( ) n i i i S v t = 则 (4)取极限 max{ , , , } 1 2 n = t t t 0 1 lim ( ) n i i i S v t → = 路程的精确值 = (3)求和

二、定积分的定义定义设函数f(x)在[a,b]上有界,在[a,b中任意插入若干个分点a= x<x <x,<…<xn-<x,=b把区间[a,b]分成n个小区间[x;-1,x;l(i=1,2,,n),各个小区间的长度为△x, = x; -xi-i(i=1,2,…),在每个小区间上任取一点5;(x;-1 ≤5,≤ x,),作乘积f(5:)△x;Zf(5,)Ax,(i=1,2,.),并作和S =i-1记a=max[△xj,Ar,,…,Ar,},如果不论对[a,b]怎样的
定义 0 1 2 1 1 1 1 1 ( ) [ , ] , [ , ] [ , ] [ , ]( 1,2, , ), ( 1,2, ), ( ), ( ) ( 1,2, ), ( ) , max{ n n i i i i i i i i i i i n i i i f x a b a b a x x x x x b a b n x x i n x x x i x x f x i S f x x − − − − = = = = = − = = = = 设函数 在 上有界 在 中任意插入 若干个分点 把区间 成 个小区间 各个小区间的长度为 在每 个小区间上任取一点 作乘积 并作和 记 1 2 , , , }, [ , ] n x x a b 如果不论对 怎样的 二、定积分的定义