
实验2数值运算MATLAB
实验2 MATLAB 数值运算

实验目的和内容实验目的了解MATLAB中矩阵和多项式的创建,以及数值函数的建立。掌握矩阵运算,多项式运算、数值函数的运算。实验内容首先介绍MATLAB中矩阵的创建,矩阵的运算:其次介绍多项式的创建,多项式的四则运算,多项式求导、求根、求值等运算;最后介绍数值函数的建立,数值函数求值、求零点、求最大最小值、求定积分,数值函数作图等
实验目的和内容 实验目的 了解MATLAB中矩阵和多项式的创建,以及数值 函数的建立。掌握矩阵运算,多项式运算、数值函 数的运算。 实验内容 首先介绍MATLAB中矩阵的创建,矩阵的运算; 其次介绍多项式的创建,多项式的四则运算,多项 式求导、求根、求值等运算;最后介绍数值函数的 建立,数值函数求值、求零点、求最大最小值、求 定积分,数值函数作图等
一、矩阵的创建矩阵是MATLAB中的基本运算单元,MATLAB支持线性代数所定义的全部矩阵运算。在进行矩阵运算之前,首先要创建矩阵。MATLAB创建矩阵有直接输入、命令生成、利用函数创建等多种方式.1.直接输入数据元素把所有元素按行写在一个中括号内,元素之间用逗号或空格隔开,行与行之间用分号隔开。ev5u1023é14u<eu- 2923例1在MATLAB中创建矩阵A=e01ü,B=-1ve:esin2!312日172<>>A=[1,2,3,4;0,-1,3,1;7,3,1,2];>>B=[sqrt(5),1,0;2,abs(-2),9;1,2, sin(2)]>> AB=02.23611.0000329.00002.00002.000003-11.00002.00000.90932371
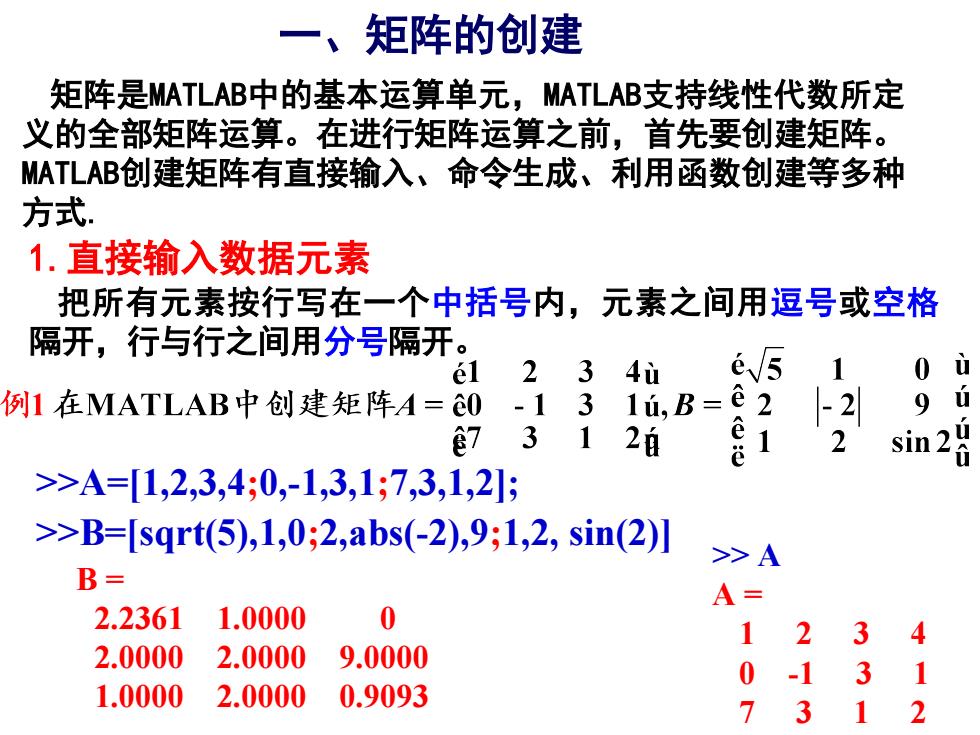
一、矩阵的创建 矩阵是MATLAB中的基本运算单元,MATLAB支持线性代数所定 义的全部矩阵运算。在进行矩阵运算之前,首先要创建矩阵。 MATLAB创建矩阵有直接输入、命令生成、利用函数创建等多种 方式. 1.直接输入数据元素 把所有元素按行写在一个中括号内,元素之间用逗号或空格 隔开,行与行之间用分号隔开。 >>A=[1,2,3,4;0,-1,3,1;7,3,1,2]; >> A A = 1 2 3 4 0 -1 3 1 7 3 1 2 >>B=[sqrt(5),1,0;2,abs(-2),9;1,2, sin(2)] B = 2.2361 1.0000 0 2.0000 2.0000 9.0000 1.0000 2.0000 0.9093

例2查看例1矩阵A中第2行第3列的元素,并将其修改为-3乘以原来的数。>>A(2,3)ans =30>> A(2,3)=(-3)*A(2,3)723A?132
例2 查看例1矩阵A中第2行第3列的元素,并将其修改 为-3乘以原来的数。 >> A A = 1 2 3 4 0 -1 3 1 7 3 1 2 >>A(2,3) ans = 3 >> A(2,3)=(-3)*A(2,3) A= 1 2 3 4 0 -1 -9 1 7 3 1 2

2.命令生成等步长向量利用“:”运算符生成等步长(均匀等分)的行向量,格式如下:a=m:p:n其中m,n,p为标量,分别代表向量的初值、终值和步长,p为1时可缺省例3向量和矩阵生成举例>>c3= -2*c2>> b1=1:10c3 =b1=-22 -14-612345678910>> x1=(0:0.3:1)*pi>>c=[c1;c2;c3]x1 =c=00.90001.80002.7000531>>c1= 5:-2:1>>c2=2*c1+13711c1=c2 =-22-14-653111 73
2.命令生成等步长向量 利用“:”运算符生成等步长(均匀等分)的行向量,格式如下: a=m:p:n 其中m, n, p为标量,分别代表向量的初值、终值和步长,p为1 时可缺省. 例3 向量和矩阵生成举例 >> b1=1:10 b1= 1 2 3 4 5 6 7 8 9 10 >> x1=(0:0.3:1)*pi x1 = 0 0.9000 1.8000 2.7000 >>c1= 5:-2:1 c1= 5 3 1 >>c2=2*c1+1 c2 = 11 7 3 >>c3= -2*c2 c3 = -22 -14 -6 >>c=[c1;c2;c3] c = 5 3 1 11 7 3 -22 -14 -6