
练习题判断下列二元函数当(α,y)一→(0,0)时二重极限与累次极限的存在性,由此可以得出二重极限存在性与两个累次极限存在性之间有什么样的关系?acyC-(1) f(α,y) =(2)Ta+y+yT1(3) f(α,y) =(α +y) sinsinay

练习参考解答-y?22ay(1) f(a,y) =(2) f(α,y)a?+y?a?+y?1lim f(x,y)lim lim f(x,y),lim lim f(x,y)(3) f(α, y) = (α + y)sin=sinx@X0yRyoxeXoXRXoyyyByOlim lim f(x,y)= lim lim f(x,y)= 0()lim f(x,y)= lim cosq sinqX@OPR0JROxROx@0TROJROlim lim f(x,y)= 1, lim lim f(x,y) = - 1(2)lim f(x,y)= limcos? g - sin?S2XROyROJROxRx@0r?0*PRO10e1111lim lim&x sinsin(3)o%y sin-sin(x+y)sin-sinRy@OxROJ1JxxyQ如果它们都存在,则三者相等仅知其中一个存在,推不出其它二者存在
练习参考解答 Ø 如果它们都存在,则三者相等 Ø 仅知其中一个存在,推不出其它二者存在

第6讲多元函数微分法及其应用李海玲山东理工大学
第6讲 多元函数微分法及其应用 山东理工大学 李海玲

一、几个基本概念及相互关系与计算多元函数偏导数的计算三、多元函数的几何应用四、多元函数的极值与最值
l 一、几个基本概念及相互关系与计算 l 二、多元函数偏导数的计算 l 三、多元函数的几何应用 l 四、多元函数的极值与最值
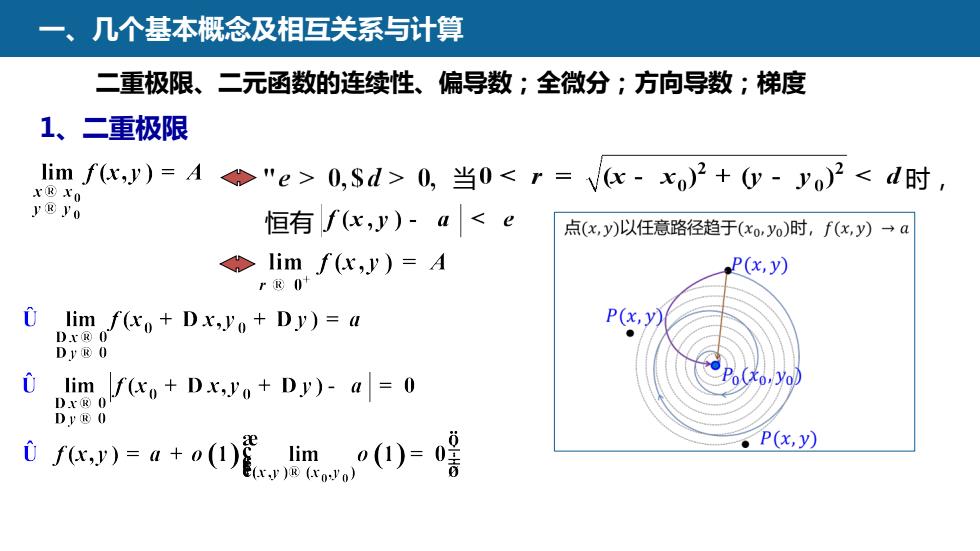
一、几个基本概念及相互关系与计算二重极限、二元函数的连续性、偏导数;全微分;方向导数;梯度1、二重极限lim f(x,y) = A"e> 0,$d> 0, 当0<r=V(x - xo)2 + (y - o)2 < d时 ,x?xoy?yo恒有f(x,j)- a< e点(x,y)以任意路径趋于(xo,yo)时,f(x,y)→alim f(x,y) = AP(x,y)rRO0P(x,y)limf(x+Dx,Jo+Dy)=aDXRODVROPo(to,yo)0lim,f(xo + Dx,yo+ Dy)-a= 0DXRODyROP(x,y)0 f(x,y)= a + o()lim0(1)=E(x)R(roVo)
一、几个基本概念及相互关系与计算 当 时, 恒有 1、二重极限 二重极限、二元函数的连续性、偏导数;全微分;方向导数;梯度