
1单调递增练习题1:设f(a)是在(a,+)(a>(单调递增且大于0的连续函数a收敛且大于零,证明:若da收敛,则级数af(a)Q+n=u1收敛练习题2:设「u是单调增加的正项数列,试证明级数un+1un=1n+1非数学类决赛:5个非数学类初赛:8个5个数学类数学类初赛:决赛:3个
非数学类初赛: 8个 非数学类决赛:5个 数学类初赛: 5个 数学类 决赛: 3个

【第十三届初赛非数学类题】(第六题)设【α|与【b,均为正实数列,满足:α,=b,=1且bn=anbn-1-2,n=2,3,.801又设[b,】为有界数列,证明级数收敛,并求该级数的和n=iaa.an【第十届初赛非数学类题】(第七题)已知[α},[b}是正数数列,且ba+1—b,≥>0,k=1,2,,为一常数.b.b....bt00tokiaa...证明:若级数%,收敛,则级数之收敛be+1bkk=ik=18ao设。an和(第七题)b为正项级数【第四届初赛非数学类题】n=1n=l8a.1Z(1)若lim>0.则收敛;a.bn+1)an+1bnn→n=18081an(2)若 lim<0且b,发散,a.发散则1bn+1)n+bnn→1n=ln=1第二届初赛第四题,第五届、第十二届初赛第七题
第二届初赛第四题,第五届、第十二届初赛第七题

第8讲无穷级数李海玲山东理工大学
第8讲 无穷级数 山东理工大学 李海玲

常数项级数敛散性的判定一一函数项级数与幂级数的收敛域与和函数二三函数的幂级数展开及其应用四、傅里叶级数及敛散性的判定
l 一、常数项级数敛散性的判定 l 二、函数项级数与幂级数的收敛域与和函数 l 三、函数的幂级数展开及其应用 l 四、傅里叶级数及敛散性的判定
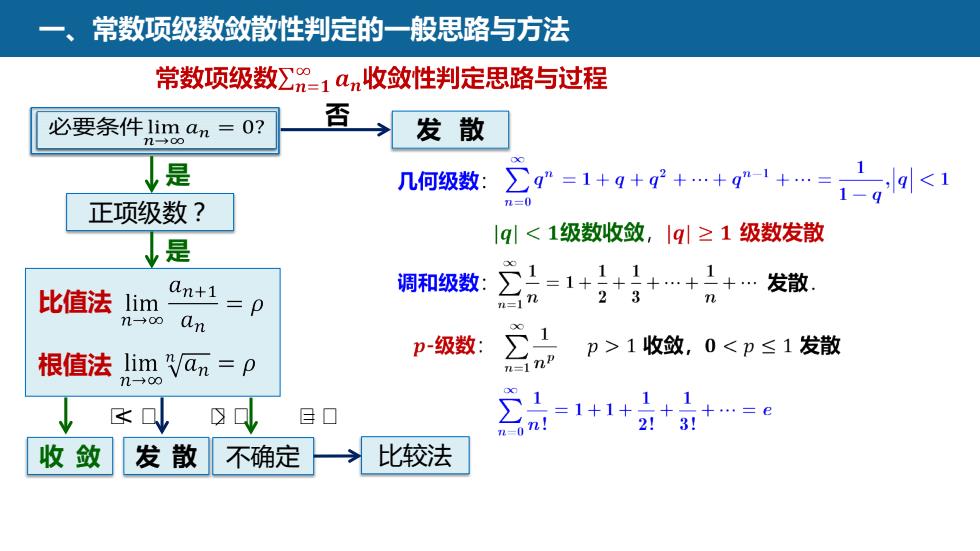
常数项级数敛散性判定的一般思路与方法常数项级数Z=1an收敛性判定思路与过程否必要条件liman=0?发散m是q"=1+q+q+..+q"-|+=g几何级数n=0正项级数?[ql<1级数收敛,Iql≥1级数发散是x111调和级数发散1+an+i23nn=in比值法limDn-→00an12p-级数p>1收敛,0<p≤1发散n=inu根值法limnan=pn-821=1+1+1+1++=e贝旦口2!3!n收敛比较法发散不确定
一、常数项级数敛散性判定的一般思路与方法 否 收 敛 正项级数? 发 散 是 是 比值法 根值法 ᵼ< ᵼ 发 散 ᵼ> ᵼ 不确定 ᵼ= ᵼ 比较法