
考研真题数学二,7分设f(x) = sin x - ( (x -t)f(t)dt,积分方程其中伪连续函数求f(x)解 (f(x)-( sinx-"(x-t)f(t)dt F'(x) =cos x - (xJ" f(t)dt- J" tf(t)dt )= cos x -(f f(t)dt + xf(x) -xf(x))= cos x - f~ f(t)dt积分方程两端再对x求导,得f"(x)=一sin x一f(x)微分方程即 y"+y=-sinx即 f"(x)+ f(x)=-sinx这是二阶常系数非齐次线性方程
考研真题数学二, 7分 = − − x f x x x t f t t 0 设 ( ) sin ( ) ( )d , 其中f为连续函数, 解 f (x) = = cos x − = − x x f t t 0 cos ( )d 两端再对x求导,得 f (x) = 求f (x). 积分方程 微分方程 = − − x f x x x t f t t 0 ( ( )) sin ( ) ( )d ( ) x 积分方程 cos x − − x tf t t 0 ( ( )d ) x ( + xf (x) x f t t 0 ( )d − xf (x) ) x x f t t 0 ( )d 即 f (x) + f (x) = −sin x 即 y + y = −sin x 这是二阶常系数非齐次线性方程. − sin x − f (x)
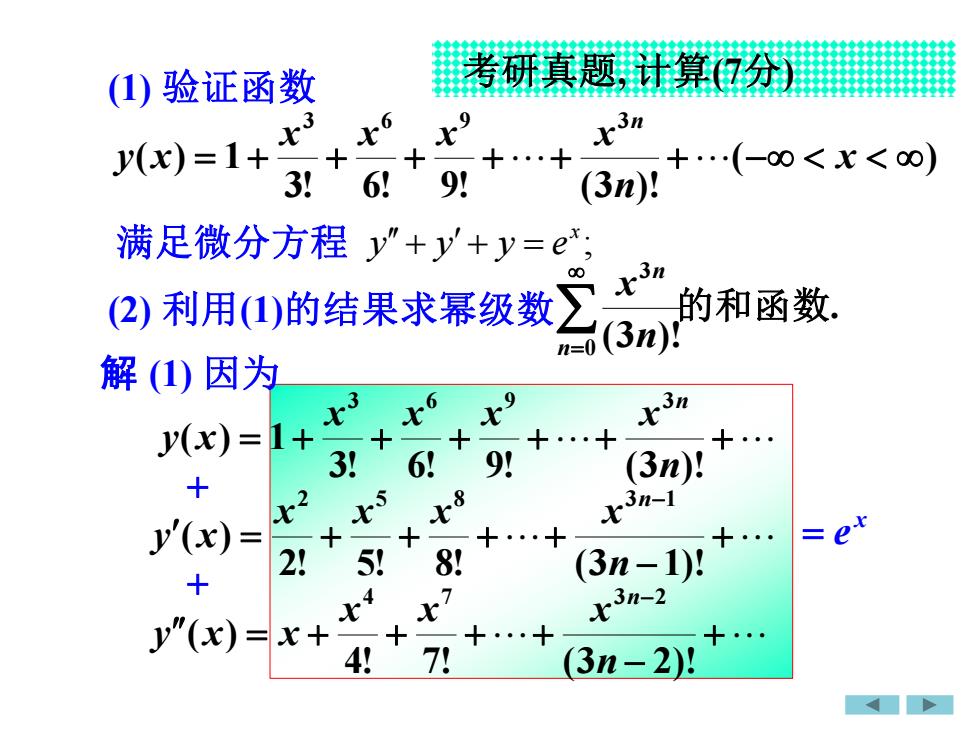
考研真题计算(7分)(1) 验证函数63mXVy(x):(-8<x<89!3!6!(3n)满足微分方程y"+y'+y=.3n8xZ的和函数。(2) 利用(1)的结果求幂级数(3n)!n=0解(1)因为t.3nt6北xy(x) =1++3!6!9!(3n)!+2.3n-1XXYx0=y(x) =2!8!5!(3n-1)!+4.3n-2x7Yy"(x)x+4!7!(3n-2)!
考研真题, 计算(7分) (1) 验证函数 ( ) 3! 6! 9! (3 )! ( ) 1 3 6 9 3 = + + + + + + − x n x x x x y x n 满足微分方程 (2) 利用(1)的结果求幂级数 . (3 )! 0 3 的和函数 n= n n x 解 (1) 因为 = + + + ++ + 3! 6! 9! (3 )! ( ) 1 3 6 9 3 n x x x x y x n + − = + + + + − 2! 5! 8! (3 1)! ( ) 2 5 8 3 1 n x x x x y x n + − = + + + + − 4! 7! (3 2)! ( ) 4 7 3 2 n x x x y x x n x = e + + ; x y y y e + + =