
第二节 微积分基本公式fundamental formula of calculus一、问题的提出二、上限函数及其导数三、牛顿一莱布尼茨公式四、小结思考题
第二节 微积分基本公式 一、问题的提出 二、上限函数及其导数 三、牛顿 — 莱布尼茨公式 四、小结 思考题 fundamental formula of calculus

一、问题的提出(v(t)和s(t)的关系)通过定积分的物理意义,找到一个计算定积分的有效、简便的方法例设某物体作直线运动,已知速度v=v(t)是时间间隔[T,T]上t的一个连续函数,且v(t)≥0,求物体在这段时间内所经过的路程T变速直线运动中路程为v(t)dt另一方面这段路程可表示为 s(T)-S(T)1其中s'(t) = v(t)v(t)dt = s(T2) - s(T)
通过定积分的物理意义, 例 变速直线运动中路程为 2 1 ( )d T T v t t 另一方面这段路程可表示为 ( ) ( ) 2 T1 s T − s (v(t)和s(t)的关系) 设某物体作直线运动,已知速度 v = v(t) [T ,T ]上t 1 2 的一个连续函数, 且v(t) 0, 求物体在这段时间内所经过的路程. 是时间间隔 ( )d ( ) ( ). 2 1 2 1 v t t s T s T T T = − s(t) = v(t) 一、问题的提出 其中 积分的有效、简便的方法. 找到一个计算定

Tv(t)dt = s(T) - s(T)JTT启发如果能从v(t)求出s(t),定积分v(t)dtT运算就可化为减法 s(T)一S(T)运算.这正是第四章已经解决了的微分运算的逆运算一不定积分问题定积分的计算有捷径可寻进行一般性的讨论
如果能从v(t)求出s(t), 2 1 ( )d T T v t t ( ) ( ) 2 T1 s T − s 这正是第四章已经解决了的微分运算的 定积分的计算有捷径可寻 进行一般性 的讨论. 运算. 定积分 运算就可化为减法 ( )d ( ) ( ) 2 1 2 1 v t t s T s T T T = − 启发 逆运算 — 不定积分问题

二、积分上限函数及其导数设f(x)在[a,b]中可积,则对任一点x E[a,b],定积分(x)=[(t)dt(J(x)dx)积分上限函数如果上限x在区间[a,b]上任意变动,则对于每一个取定的x值,定积分有一个对应值,所以它在[a,b]上定义了一个函数,记为Φ(x)注定要分清函数的自变量x与积分变量t9I
定积分 a f (t)dt 积分上限函数 x [a,b], 记为(x). 注 ( ( )d ) x a f x x 一定要分清函数的 如果上限 x 在区间[a,b]上任意变动, 每一个取定的x值, 则对于 定积分有一个对应值,所以它 在[a,b]上定义了一个函数, 设f (x)在[a,b]中可积,则对任一点 x (x) = 自变量x与积分变量t. x t t 二、积分上限函数及其导数
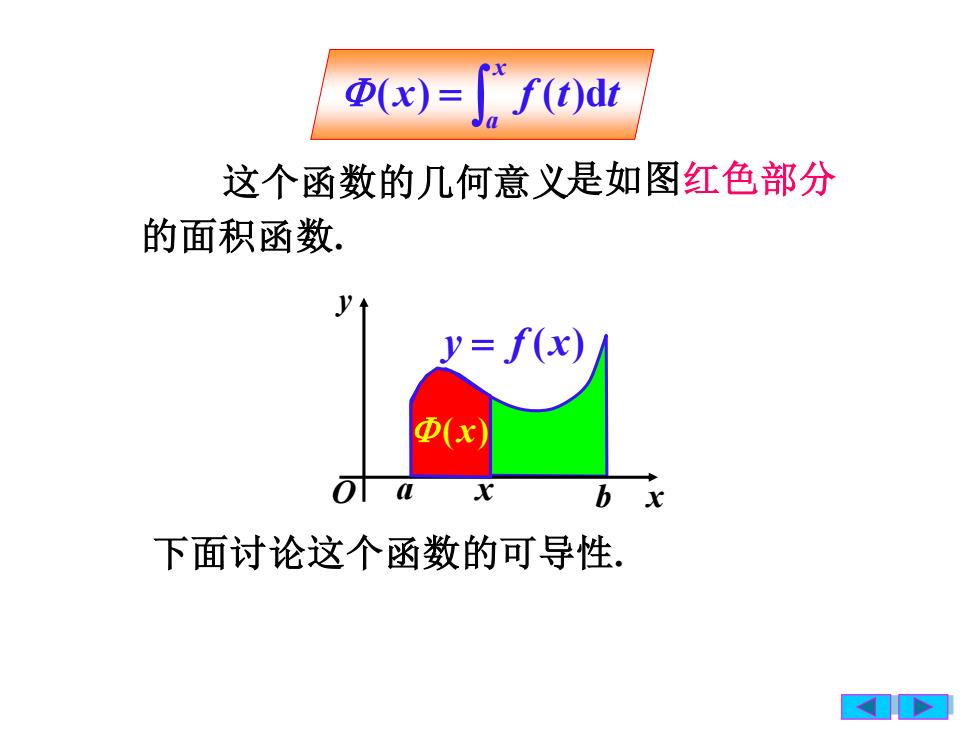
@(x)= f' f(t)dt这个函数的几何意义是如图红色部分的面积函数Vy= f(x)@(x)olaxbx下面讨论这个函数的可导性
= x a (x) f (t)dt 这个函数的几何意义 下面讨论这个函数的可导性. 是如图红色部分 的面积函数. a b y = f (x) O x y x (x)