
第一节定积分的概念与性质一、定积分问题举例二、定积分的定义三、定积分的儿何意义和物理意义四、关于函数的可积性五、定积分的性质六、小结思考题
1 第一节 定积分的概念与性质 一、定积分问题举例 二、定积分的定义 四、关于函数的可积性 三、定积分的几何意义和物理意义 六、小结 思考题 五、定积分的性质
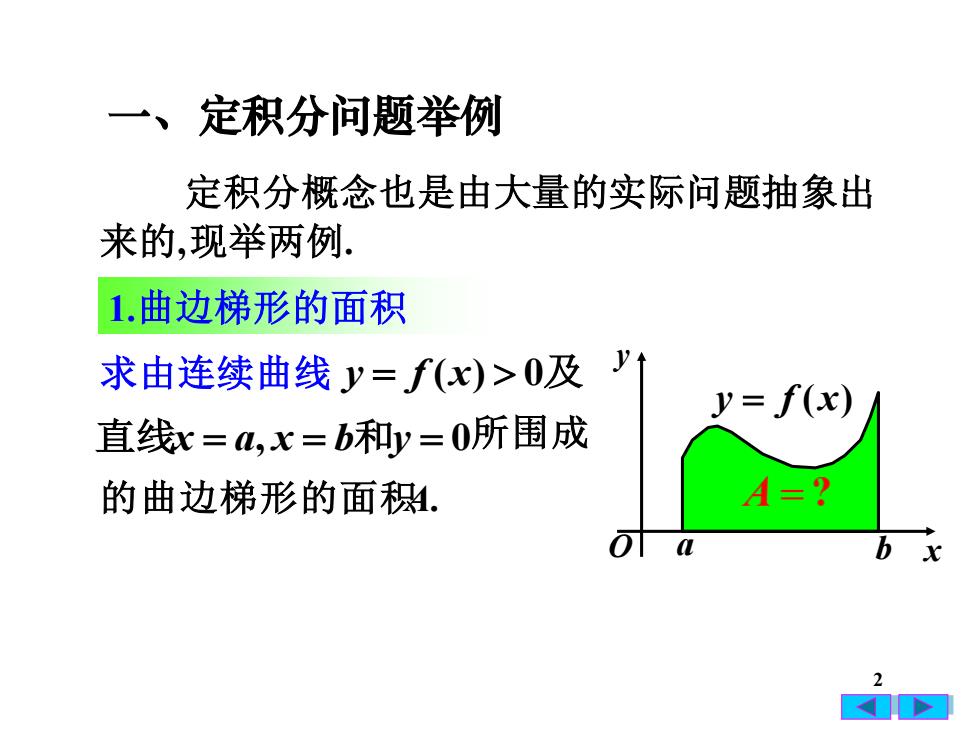
一、定积分问题举例定积分概念也是由大量的实际问题抽象出来的,现举两例。1.曲边梯形的面积求由连续曲线y=f(x)>0及y= f(x)直线x=a,x=b和y=0所围成A=的曲边梯形的面积OTabx2A
2 1.曲边梯形的面积 定积分概念也是由大量的实际问题抽象出 求由连续曲线 y = f (x) 0及 直线x = a, x = b和y = 0所围成 的曲边梯形的面积A. 一、定积分问题举例 来的, 现举两例. a b y = f (x) O x y
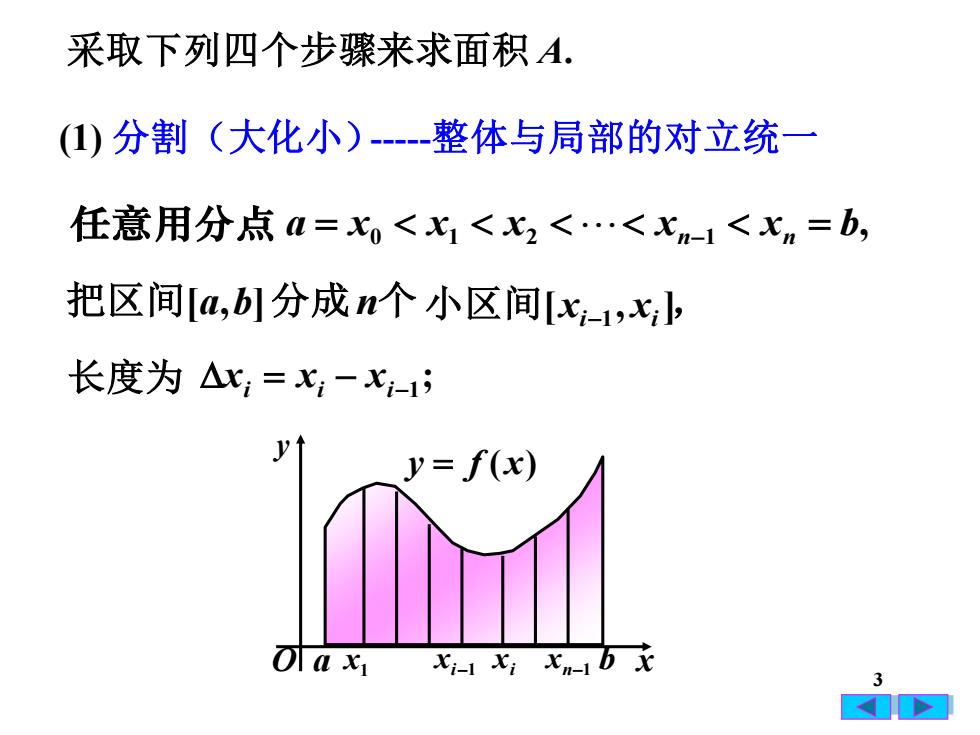
采取下列四个步骤来求面积A(1)分割(大化小)-----整体与局部的对立统一任意用分点 a= X<xi <x <.….<xn-1 <x=b,把区间[a,b]分成n个小区间[xi-1,x;l,长度为 △x; =X;-Xi-1Jy= f(x)ofa xiXi-X,X-b3A
3 把区间[a,b]分成n个 采取下列四个步骤来求面积 A. (1) 分割(大化小) , 任意用分点 a = x0 x1 x2 xn−1 xn = b ; xi = xi − xi−1 小区间[xi−1 , xi ], 长度为 a b y = f (x) O x y x1 xi−1 xi xn−1 -整体与局部的对立统一
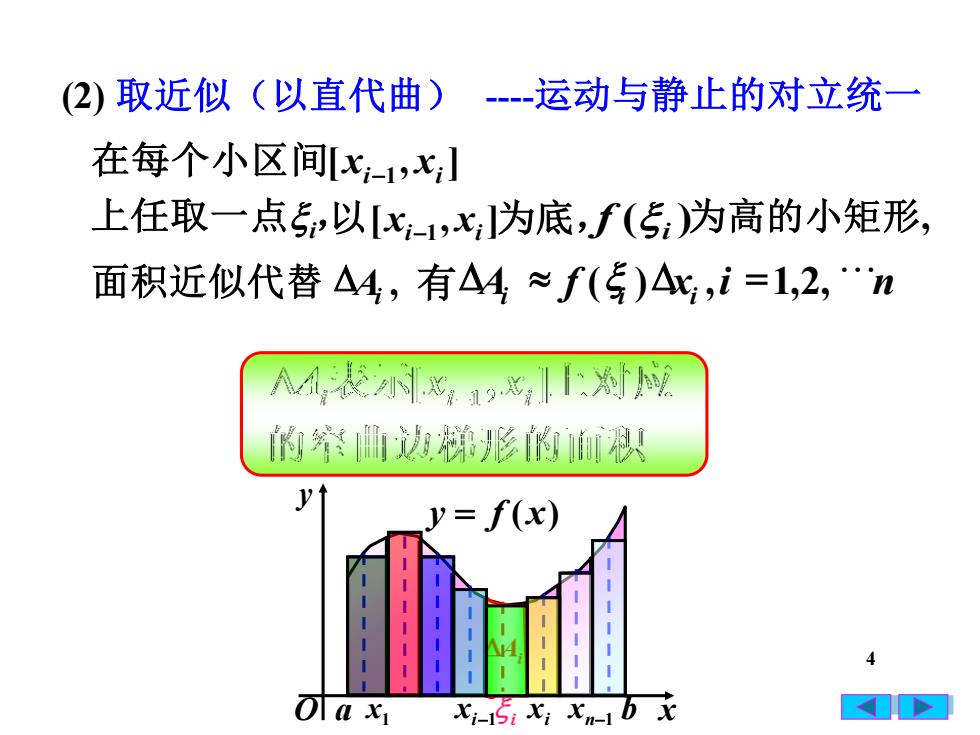
(2)取近似(以直代曲)----运动与静止的对立统一在每个小区间[x;-1,x;]上任取一点5,以[xi-1,x;I为底,f(;)为高的小矩形,面积近似代替 AA,有A,~f()Ax;,i=1,2,nM表x1x心维山边梯形的棋Vy= f(x)ofa xX-15, x; x-b xA
4 a b y = f (x) [ , ] 在每个小区间 xi−1 xi (2) 取近似(以直代曲) 以[xi−1 , xi ]为底, ( )i f 为高的小矩形, 面积近似代替 O x y i x 1 x i−1 x n−1 x 上任取一点 i, Ai , 有Ai f (i )xi ,i =1,2,n -运动与静止的对立统一
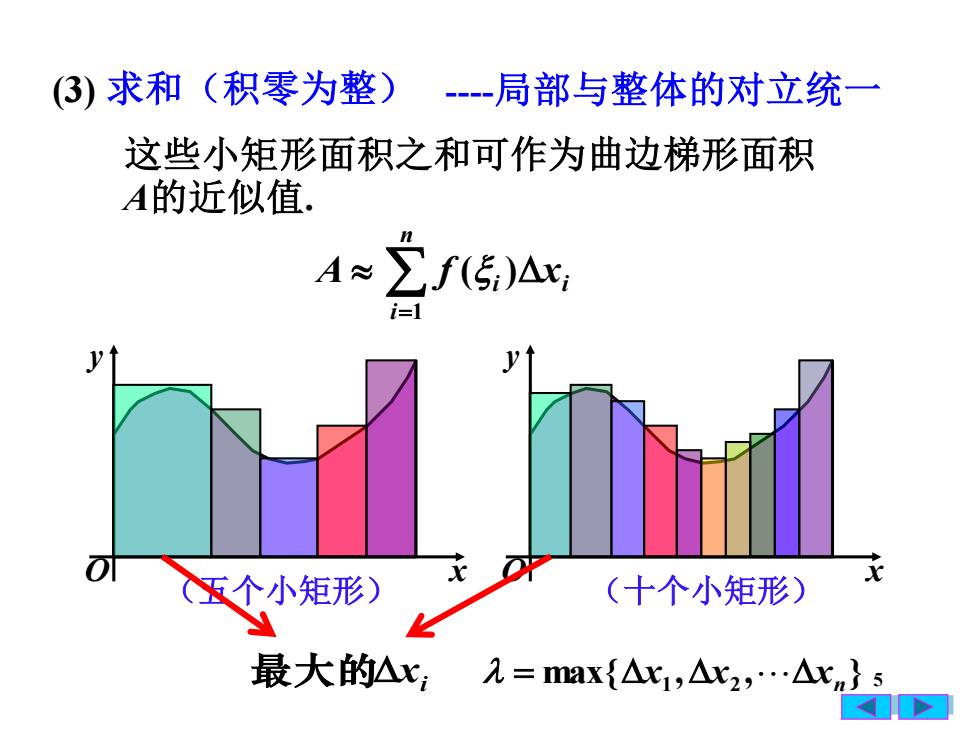
(积零为整)(3) 求和----局部与整体的对立统一这些小矩形面积之和可作为曲边梯形面积A的近似值1Zf(5)Ax;A~i-1yVotxOx(工个小矩形)(十个小矩形)最大的△x;a = max(Axj,Ax2, ...Axn]A
5 A (3) 求和(积零为整) 这些小矩形面积之和可作为曲边梯形面积 A的近似值. i n i f i x = ( ) 1 (五个小矩形) (十个小矩形) O x y O x y 最大的xi max{ , , } = x1 x2 xn -局部与整体的对立统一