
第一节定积分的元素法、问题的提出思考题二、 小结
第一节 定积分的元素法 一、问题的提出 二、小结 思考题 1
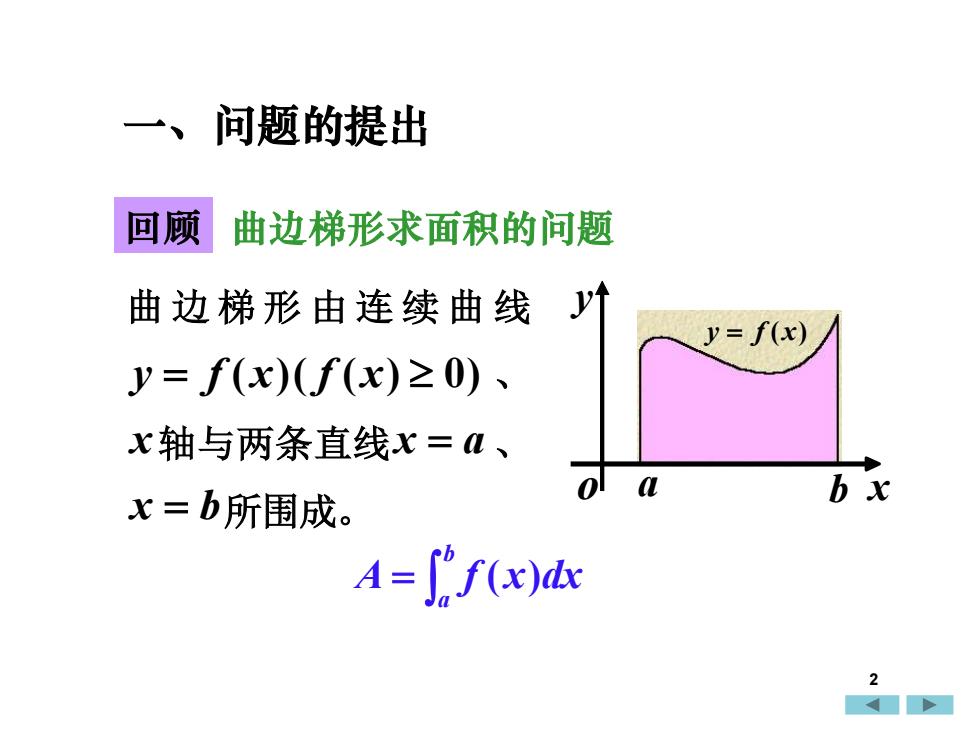
问题的提出、回顾曲边梯形求面积的问题yt曲边梯形由连续曲线y= f(x)y= f(x)(f(x)≥0) ~x轴与两条直线x=a、01ab xx=b所围成。A = f'f(x)dx2
回顾 曲边梯形求面积的问题 = b a A f (x)dx 一、问题的提出 曲 边 梯 形 由 连 续 曲 线 y = f (x)( f ( x) 0) 、 x轴与两条直线x = a 、 x = b所围成。 a b x y o y = f (x) 2

面积表示为定积分的步骤如下(1)把区间[a,bl分成n个长度为△x,的小区间相应的曲边梯形被分为n个小窄曲边梯形,第i个小窄曲边梯形的面积为△A,则A=△A,i=1(2)计算△A,的近似值A, ~ f(5)Ax5; EAx;(3)求和,得A的近似值 A~f(5)Ax;i13
面积表示为定积分的步骤如下 (1)把区间[a,b]分成n个长度为xi 的小区间, 相应的曲边梯形被分为n个小窄曲边梯形,第i 个小窄曲边梯形的面积为Ai,则 = = n i A Ai 1 . (2)计算Ai 的近似值 i i xi A f ( ) i xi (3) 求和,得A的近似值 ( ) . 1 i i n i A f x = 3
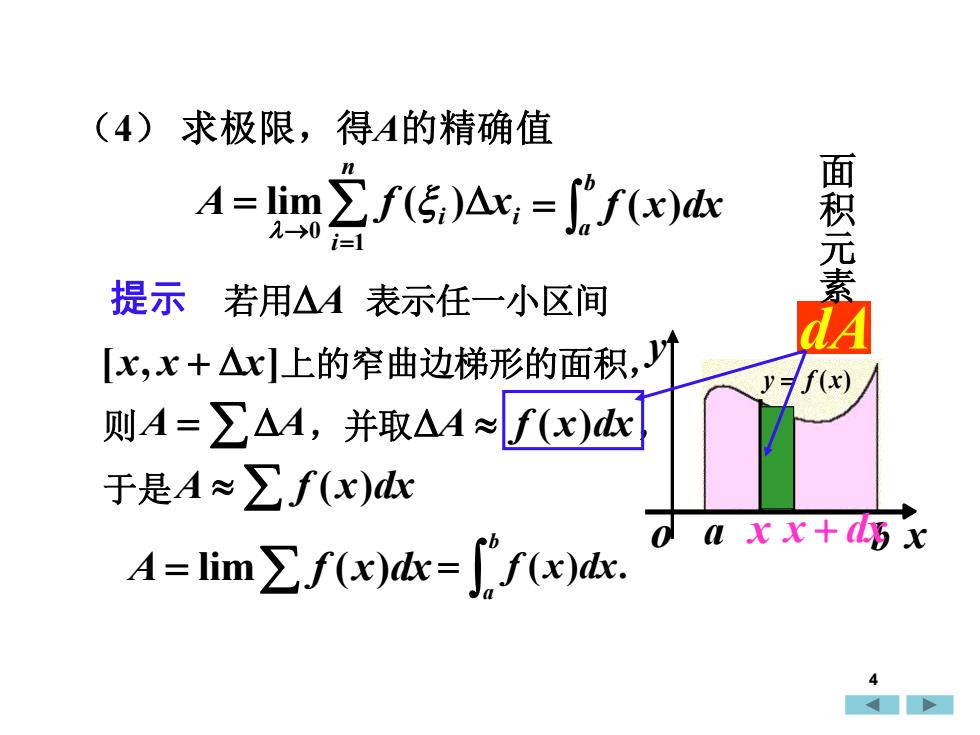
(4)求极限,得A的精确值面积元素nA = limZ f(5)Ax; = f' f(x)dx2-→0i=1提示若用△A表示任一小区间dA[x,x+Ax]上的窄曲边梯形的面积,Jf(x)则A=Z△A,并取△A~f(x)dx于是A~f(x)dxxx+dx0axA = lim Z f(x)dx= / f(x)dx.4
a b x y o y = f (x) (4) 求极限,得A的精确值 i i n i A = f x = → lim ( ) 1 0 = b a f (x)dx 提示 若用A 表示任一小区间 [x, x + x]上的窄曲边梯形的面积, 则A = A,并取A f ( x)dx, 于是A f (x)dx A = lim f (x)dx ( ) . = b a f x dx x x + dx dA 面 积 元 素 4

当所求量U符合下列条件:(1)U 是与一个变量x 的变化区间a,b|有关的量;(2)U对于区间a,b具有可加性,就是说,如果把区间a,b分成许多部分区间,则U相应地分成许多部分量,而U等于所有部分量之和;(3)部分量△U,的近似值可表示为f()△x;就可以考虑用定积分来表达这个量U5
当所求量U 符合下列条件: (1)U 是与一个变量x 的变化区间a,b 有关 的量; (2)U 对于区间a,b具有可加性,就是 说,如果把区间a,b分成许多部分区间,则 U 相应地分成许多部分量,而U 等于所有部 分量之和; (3)部分量Ui的近似值可表示为 i xi f ( ) ; 就可以考虑用定积分来表达这个量U 5