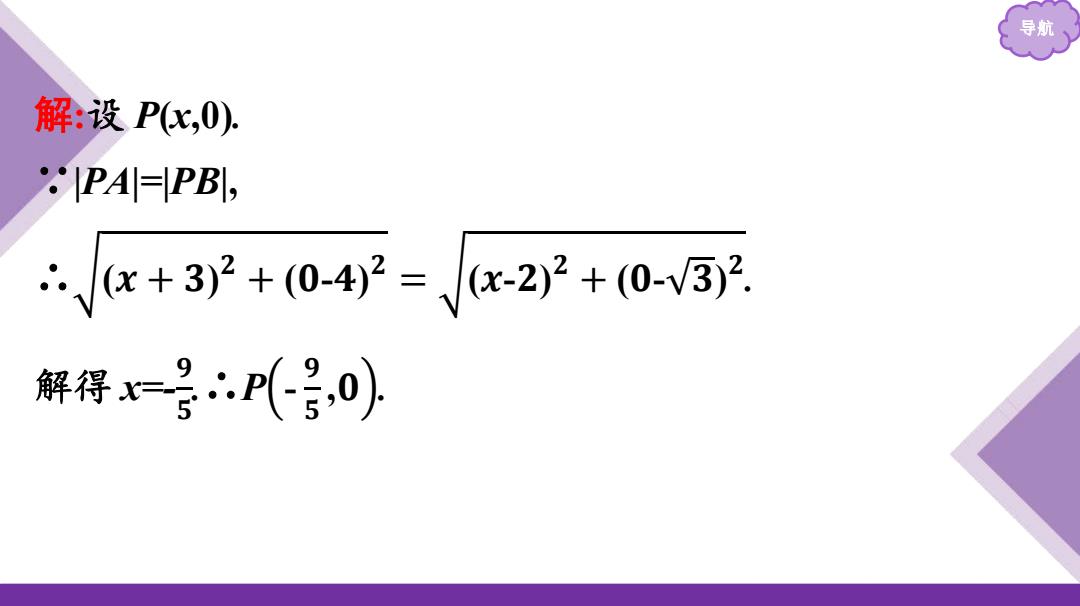
导航 解:设P飞,0) PA=PBI, ∴(x+32+(0-42=、(x-2)2+(0-V32 解得x=P(-号,0)
导航 解:设 P(x,0). ∵|PA|=|PB|, ∴ (𝒙 + 𝟑) 𝟐 + (𝟎-𝟒) 𝟐 = (𝒙-𝟐) 𝟐 + (𝟎- 𝟑) 𝟐 . 解得 x=- 𝟗 𝟓 .∴P - 𝟗 𝟓 ,𝟎

导 反思感悟 1.两点之间的距离公式可以变形为AB2=(x1-x2)2+(y1y2)2. 2.在涉及求平方和的最小值的问题时,可通过两点之间的距离 公式的形式进行构造变形,利用动点到定点的最小距离求解. 3.利用两点之间的距离公式可以判断三角形的形状,从三角形 的三边长入手,根据边长相等判断是等腰三角形或等边三角 形,根据勾股定理判断是直角三角形
导航 1.两点之间的距离公式可以变形为|AB|2=(𝒙𝟏−𝒙𝟐) 𝟐+(y1 -y2 ) 2 . 2.在涉及求平方和的最小值的问题时,可通过两点之间的距离 公式的形式进行构造变形,利用动点到定点的最小距离求解. 3.利用两点之间的距离公式可以判断三角形的形状,从三角形 的三边长入手,根据边长相等判断是等腰三角形或等边三角 形,根据勾股定理判断是直角三角形

导 【变式训练1】已知A(2,1),B(6,3),C1,3),求证:△ABC为直角 三角形. 证明:由已知,得 AB=V16+4=2V5,BC=V25+0=5,4C=V1+4=V5. .AB2+AC2-BC, .△ABC为直角三角形
导航 【变式训练1】已知A(2,1),B(6,3),C(1,3),求证:△ABC为直角 三角形. 证明:由已知,得 ∵|AB|2+|AC|2=|BC|2 , ∴△ABC为直角三角形. |AB|= 𝟏𝟔 + 𝟒=2 𝟓,|BC|= 𝟐𝟓 + 𝟎=5,|AC|= 𝟏 + 𝟒 = 𝟓