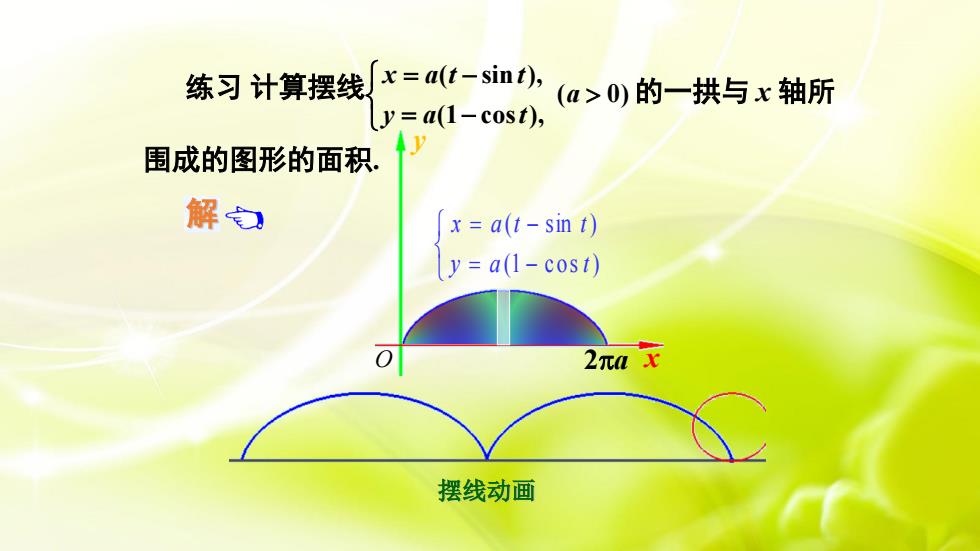
x = a(t-sint),练习计算摆线(a>0)的一拱与x轴所ly = a(1-cost),围成的图形的面积解台x =a(t-sin t)y=a(l-cost)02元aX摆线动画
x y O 2a = − = − (1 co s ) ( sin ) y a t x a t t 练习 计算摆线 第二节 定积分在几何上的应用 围成的图形的面积. 解 例4 计算摆线 ( 0) 的一拱与 x 轴所 (1 cos ), ( sin ), = − = − a y a t x a t t 所求面积为 = a A y x 2π 0 d = − − a a t a t t 2π 0 (1 cos )d[ ( sin )] = − 2π 0 2 2 a (1 cost) dt 3π . 2 = a x y O 2a = − = − (1 cos ) ( sin ) y a t x a t t ( 0) 的一拱与 x 轴所 (1 cos ), ( sin ), = − = − a y a t x a t t 围成的图形的面积. 摆线动画

思政时刻一摆线欣赏性质性质1从图中可以看出,摆线的图形具有周期性,周期为2元a性质2每一拱有一个最高点:x=(2k-1)元a,拱高为2a。性质3一拱的弧长为8a,是旋转圆直径的4倍,更神奇的是其长度是与元无关的有理数
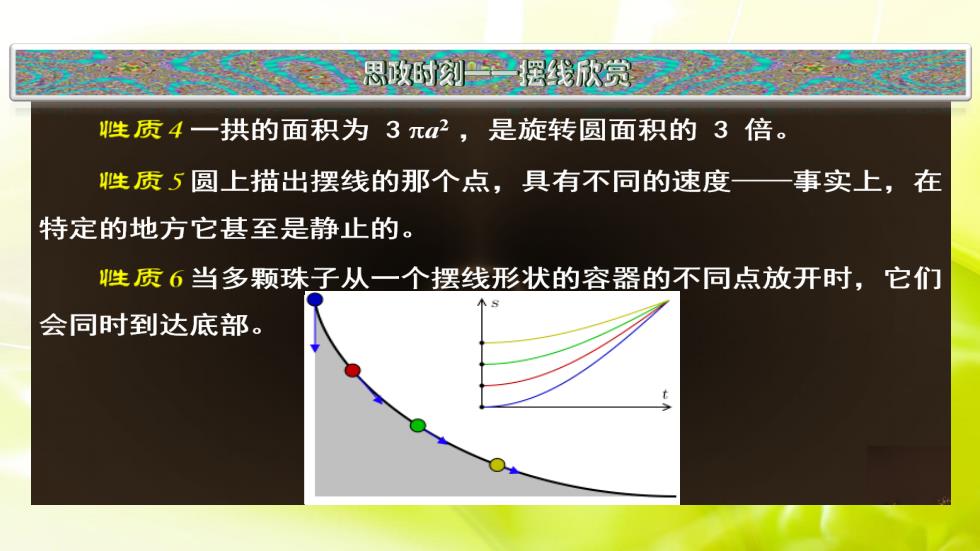
思政时刻摆线欣赏性质4一拱的面积为3元a,是旋转圆面积的3倍。事实上,在性质5圆上描出摆线的那个点,具有不同的速度特定的地方它甚至是静止的。性质6当多颗珠子从一个摆线形状的容器的不同点放开时,它们会同时到达底部
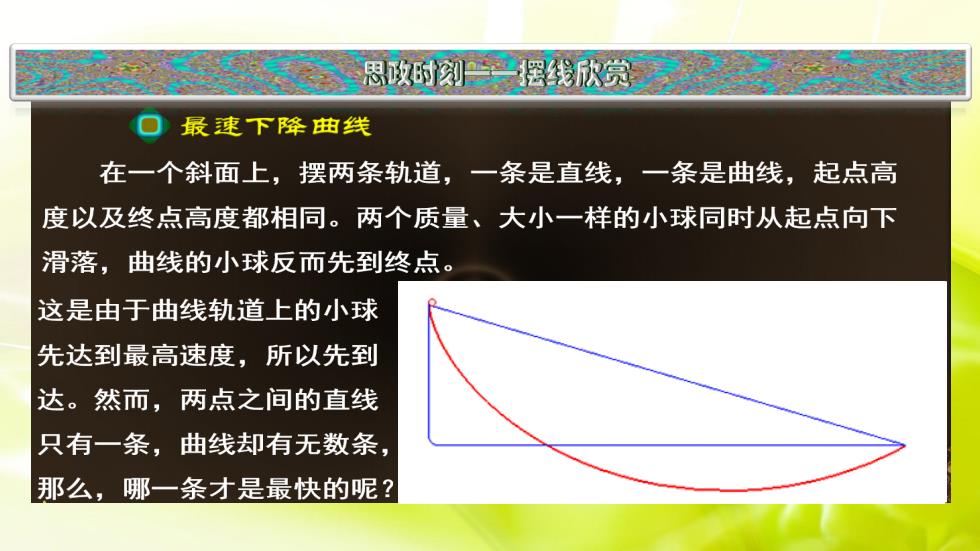
思政时刻一摆线欣赏最速下降曲线在一个斜面上,摆两条轨道,一条是直线,一条是曲线,起点高度以及终点高度都相同。两个质量、大小一样的小球同时从起点向下滑落,曲线的小球反而先到终点,这是由于曲线轨道上的小球先达到最高速度,所以先到达。然而,两点之间的直线只有一条,曲线却有无数条那么,哪一条才是最快的呢?
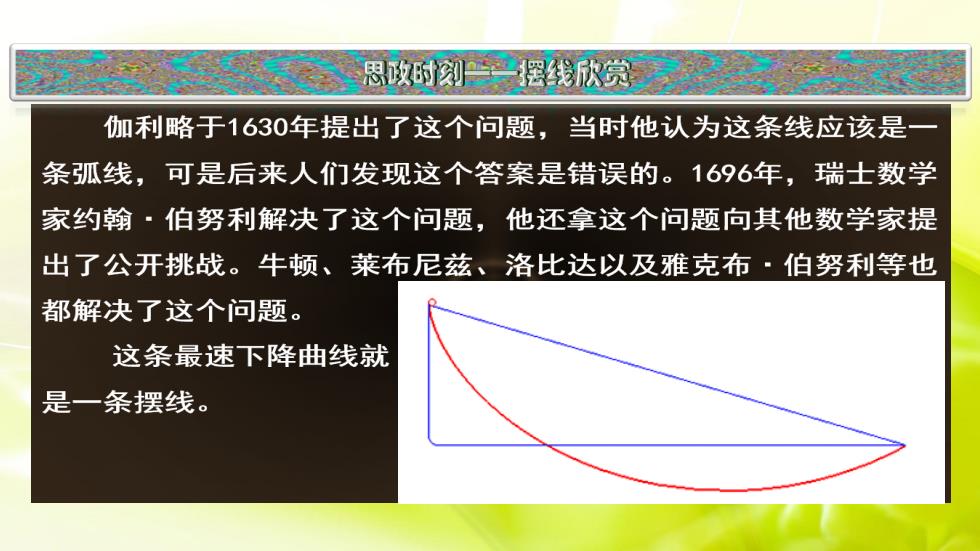
思政时刻摆线欣赏伽利略于1630年提出了这个问题,当时他认为这条线应该是条弧线,可是后来人们发现这个答案是错误的。1696年,瑞士数学家约翰·伯努利解决了这个问题,他还拿这个问题向其他数学家提出了公开挑战。牛顿、莱布尼兹、洛比达以及雅克布伯努利等也都解决了这个问题。这条最速下降曲线就是一条摆线