《高等数学》课程教学资源（课件讲稿）第六章_6.2定积分在几何上的应用

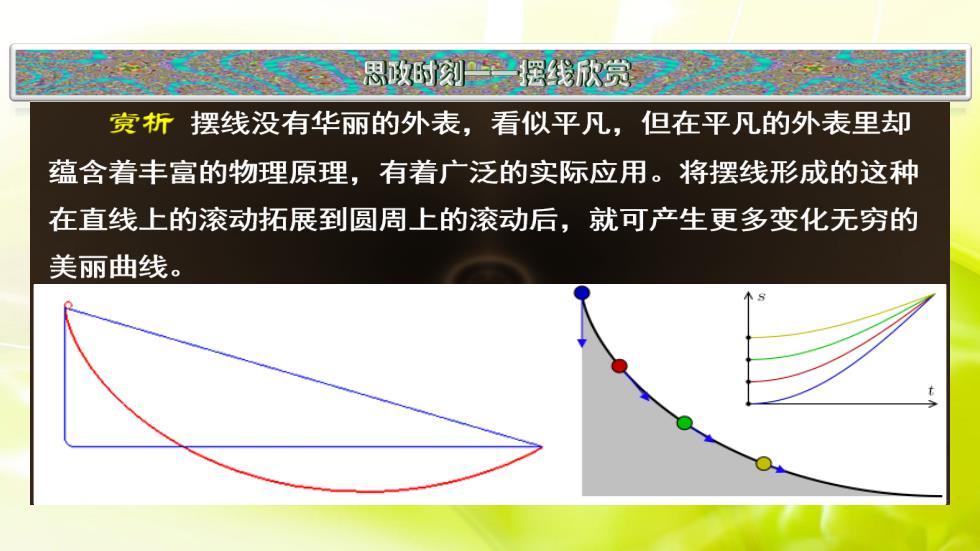
思政时刻摆线欣赏赏析摆线没有华丽的外表，看似平凡，但在平凡的外表里却蕴含着丰富的物理原理，有着广泛的实际应用。将摆线形成的这种在直线上的滚动拓展到圆周上的滚动后，就可产生更多变化无穷的美丽曲线

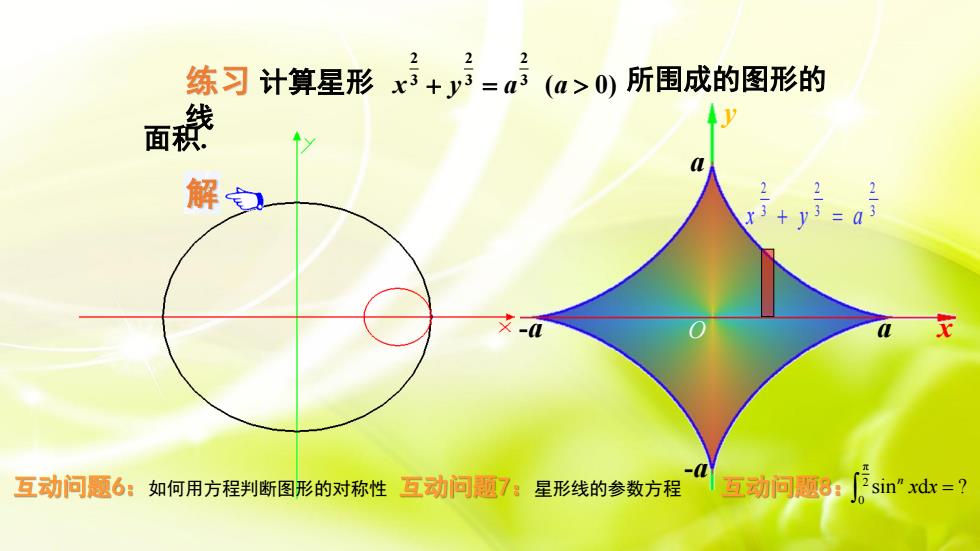
x+y=a (a>0) 所围成的图形的练习计算星形线面积a解之XX-aa2互动问题6！互动问题7互动问题8：sin"xdx=?如何用方程判断图形的对称性星形线的参数方程Jo

练习 计算星形 线 第二节 定积分在几何上的应用 3 2 3 2 3 2 x + y = a -a a -a a x y O 解 例5 计算星形线 3 ( 0) 所围成的图形的 2 3 2 3 2 x + y = a a  面积. 星形线的参数方程为 (0 2π). sin , cos , 3 3      = = t y a t x a t 由对称性可得  = a A y x 0 4 d  = 0 2 π 3 3 4 asin td(a cos t)  = 2 π 0 2 4 2 4a sin t cos tdt  = − 2 π 0 2 4 6 4a (sin t sin t)dt π . 8 3 2 = a 3 ( 0) 所围成的图形的 2 3 2 3 2 x + y = a a  面积. 3 2 3 2 3 2 x + y = a -a a -a a x y O 互动问题7：星形线的参数方程 互动问题8： π 2 0 sin d ? n x x = 互动问题6：如何用方程判断图形的对称性 

2、极坐标系情形0+de设由曲线p=β()及射线p=p(0)θ=β=α、=围成一曲边扇形de求其面积.这里β(0)在[α,β上连续，且β()≥0.x0=α面积元素dA=0(0)dee只 A=[,(g(0)"d0.曲边扇形的面积

o x  =  d  =    + d 面积元素 dA   d 2 [ ( )] 2 1 = 曲边扇形的面积 [ ( )] . 2 1 2      A d  =    = ( ) 2、极坐标系情形 ( ) . ( ) [ , ] ( ) 0.              = = =  设由曲线 及射线 、 围成一曲边扇形， 求其面积 这里 在 上 连续，且

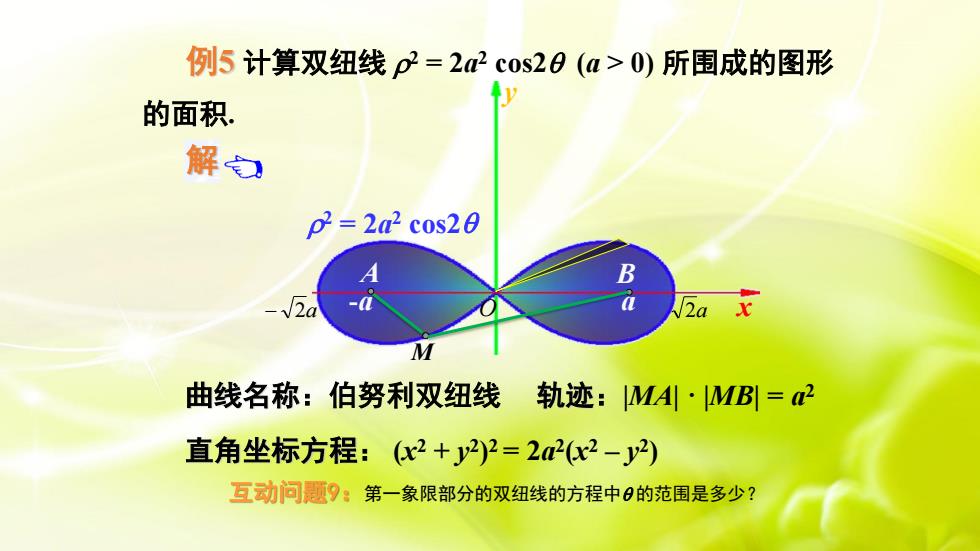
例5计算双纽线p=2a2cos2（a>0)所围成的图形的面积解白p =2a?cos20Ba-V2a-aN2aYM曲线名称：伯努利双纽线轨迹：[MAI·[MBI=α2直角坐标方程：(x2+y2)2=2a(x2-y)互动问题9：第一象限部分的双纽线的方程中e的范围是多少？

例5 计算双纽线  2 = 2a 2 cos2 (a > 0) 所围成的图形 第二节 定积分在几何上的应用 x y  2 = 2a 2 cos2 -a a − 2a 2a M A B O 解 例8 计算双纽线  2 = 2a 2 cos2 (a > 0) 所围成的图形 的面积. 由对称性，  =  4 π 0 2 ( )d 2 1 A 4     = 4 π 0 2 4 a cos 2d 2 . 2 = a 的面积. 曲线名称：伯努利双纽线 轨迹：|MA| · |MB| = a 2 直角坐标方程： (x 2 + y 2 ) 2 = 2a 2 (x 2 – y 2 ) x y  2 = 2a 2 cos2 -a a − 2a 2a M A B O 互动问题9：第一象限部分的双纽线的方程中 的范围是多少？

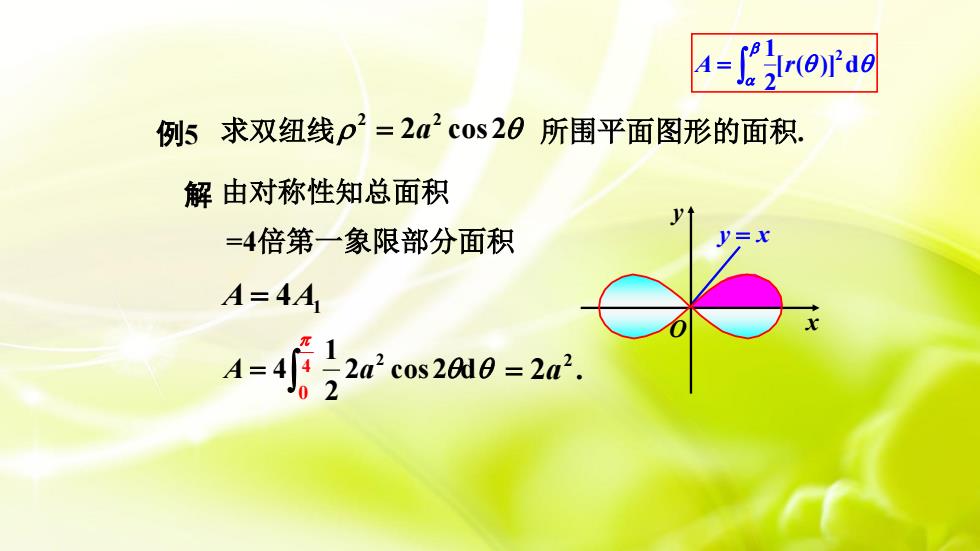
A=J2,(r(0)r'de例5求双纽线p2=2a~cos20所围平面图形的面积解由对称性知总面积一4倍第一象限部分面积A=4Ax2a2cos20d0=2a?A=2S

解 由对称性知总面积 A = 4A1 2 cos 2 d 2 1 4 2  A = a 2 . 2 = a     [ ( )] d 2 1 2 A r  = 0 4  =4倍第一象限部分面积 例5 求双纽线 2 2   = 2 cos 2 a 所围平面图形的面积. y = x O x y