
于是所求面积 A=A +A,A = f,(x3 -6x - x")dx+ f(x? - x* + 6x)dx-25312说明:注意各积分区间上被积函数的形式,问题:积分变量只能选x吗?
于是所求面积 A = A1 + A2 A (x 6x x )dx 2 0 2 3 = − − (x x 6x)dx 2 3 3 0 + − + . 12 253 = 说明:注意各积分区间上被积函数的形式. 问题:积分变量只能选 x 吗?
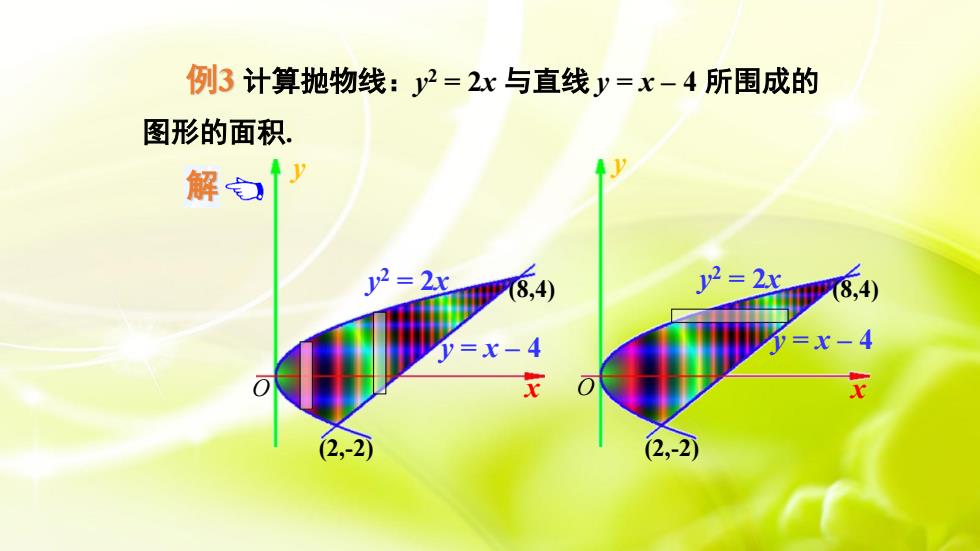
例3计算抛物线:y2=2x与直线y=x-4所围成的图形的面积解白V2=2xy2 = 2x(8.4)(8,4)V=x-4V=x-4xY(2,-2)(2,-2)
y 2 = 2x y = x – 4 x y O (2,-2) (8,4) 例3 计算抛物线:y 2 = 2x 与直线 y = x – 4 所围成的 第二节 定积分在几何上的应用 y 2 = 2x y = x – 4 x y O (2,-2) (8,4) 解 例2 计算抛物线:y 2 = 2x 与直线 y = x – 4 所围成的 图形的面积. 解方程组 = − = 4 2 2 y x y x 得抛物线和直线的交点为 (2 , -2) 和 (8 , 4) . 选 y 为积分变量,则面积元素为 d , 2 1 d 4 2 A y y y = + − 图形的面积. y 2 = 2x y = x – 4 x y O (2,-2) (8,4)

例3计算由曲线y2=2x和y=x-4所围成的图形的面积.解两曲线的交点72[y? = 2x(8,4)2y=x-4y=x-4x→ (2,-2), (8,4).(2,-2)ye[-2,4]选为积分变量dA =18.y+4-A=dA =dy-2
解 两曲线的交点 (2,−2), (8,4). = − = 4 2 2 y x y x 选 y 为积分变量 y [−2, 4] dy y dA y = + − 2 4 2 18. 42 = = − A dA 2 3 2 4 . 例 计算由曲线y x y x = = − 和 所围成的 图形的面积 y 2 = 2 xy = x – 4 x y O (2, -2) (8,4)

x=p(t)如果曲边梯形的曲边为参数方程(y=y(t)曲边梯形的面积A = ' f(x)dx = J" y(t)p'(t)dt.(其中α和β对应曲线起点和终点的参数值)在[α,β]或[β,α]上x=(t)具有连续的导数y=y(t)连续
如果曲边梯形的曲边为参数方程 = = ( ) ( ) y t x t 曲边梯形的面积 ( ) ( ) ( ) . b a A f x dx t t dt = = (其中 和 对应曲线起点和终点的参数值) [ ] [ , ] ( ) ( ) . x t y t = = 在 , 或 上 具有连续的导数, 连续
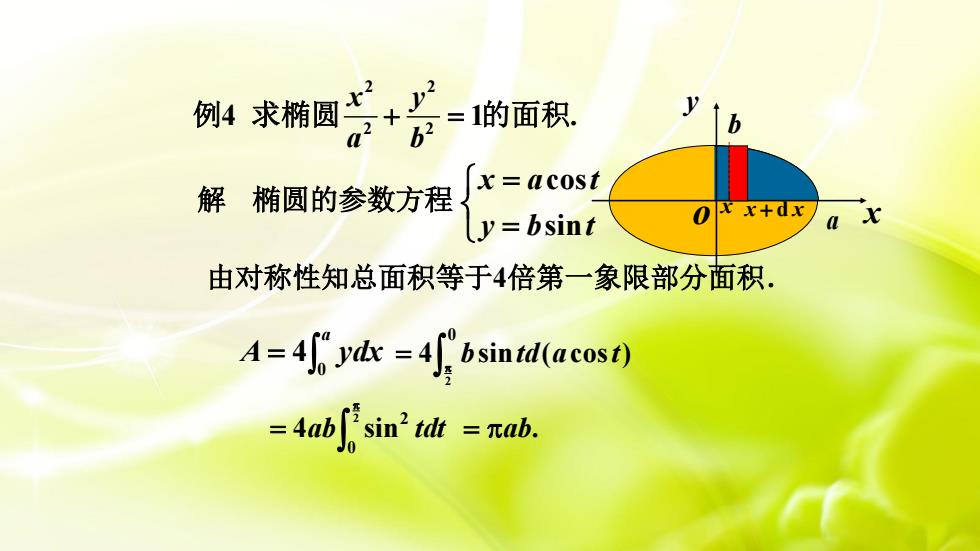
大y2例4 求椭圆1的面积.=b2x=acost解椭圆的参数方程xx+dx0北ay=bsint由对称性知总面积等于4倍第一象限部分面积。A = 4f, ydx =4f, bsintd(acost)= 4ab [' sin’ tdt = πab.J0
解 椭圆的参数方程 = = y b t x a t sin cos 由对称性知总面积等于4倍第一象限部分面积. = a A ydx 0 4 = 0 2 4 bsintd(acost) ab tdt = 2 0 2 4 sin = ab. 2 2 2 2 4 1 . x y a b 例 求椭圆 + = 的面积 a b o x y x x x + d