
上游充通大 SHANGHAI JIAO TONG UNIVERSITY 逻辑语言的例子: V国家,ヨ数值,使得:V司机:(司机酒精含量>h)→(司机在该国被判定为醉驾)。 V国家,3两个整数a1,a2,使得:V男人V女人:(男人年龄>a1)∧(女人年龄>a2) 男人和女人在该国可以合法结婚
逻辑语言的例子:

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY §2.1极限和连续性 2.1.1极限 定义(函数的极限):设函数w=f(z)在0<2-z<p内 有定义,如果有一确定的数4(≠∞)存在,对于⊙>0,目 δ>0(0<6≤p),使得 0<2-zK8 f(-4 则称A为f(z)当z趋向于z时的极限,记作 lim f(z)=4 z→20 或记作当z→z时,f(2)→A
定义(函数的极限): 设函数 w = f (z) 在 0 < |z−z0| < ρ 内 有定义, 如果有一确定的数A(≠∞)存在, 对于 δ >0 (0 <δ ≤ρ), 使得 0 <|z−z0|<δ | f (z)−A |<ε , 则称A为f (z)当 z趋向于z0时的极限, 记作 f z A z z = → lim ( ) 0 或记作当 z→z0 时 , f (z)→A. 2.1.1 极限 ∀ε > 0, ∃ ⇒ § 2.1 极限和连续性
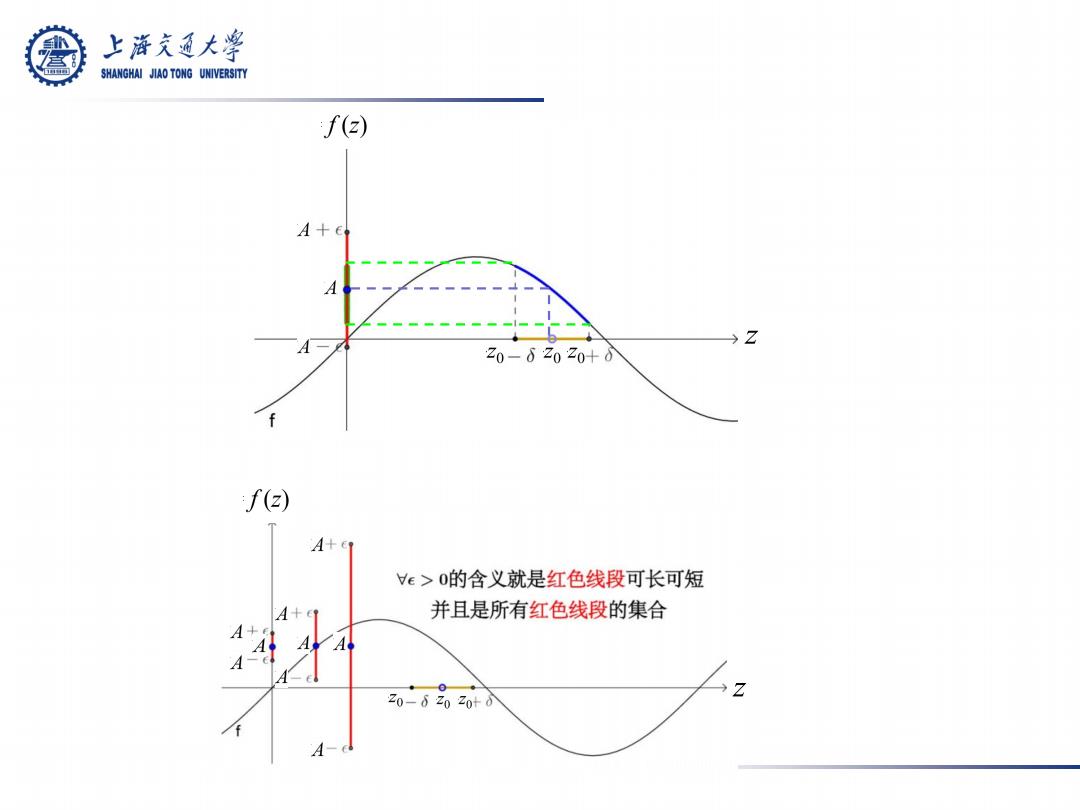
上游充通大学 SHANGHAI JIAO TONG UNIVERSITY /C) A+6 →Z 20-62020+0d A+ e>0的含义就是红色线段可长可短 A+1 并且是所有红色线段的集合 A+ A年A 20-62020+0 A
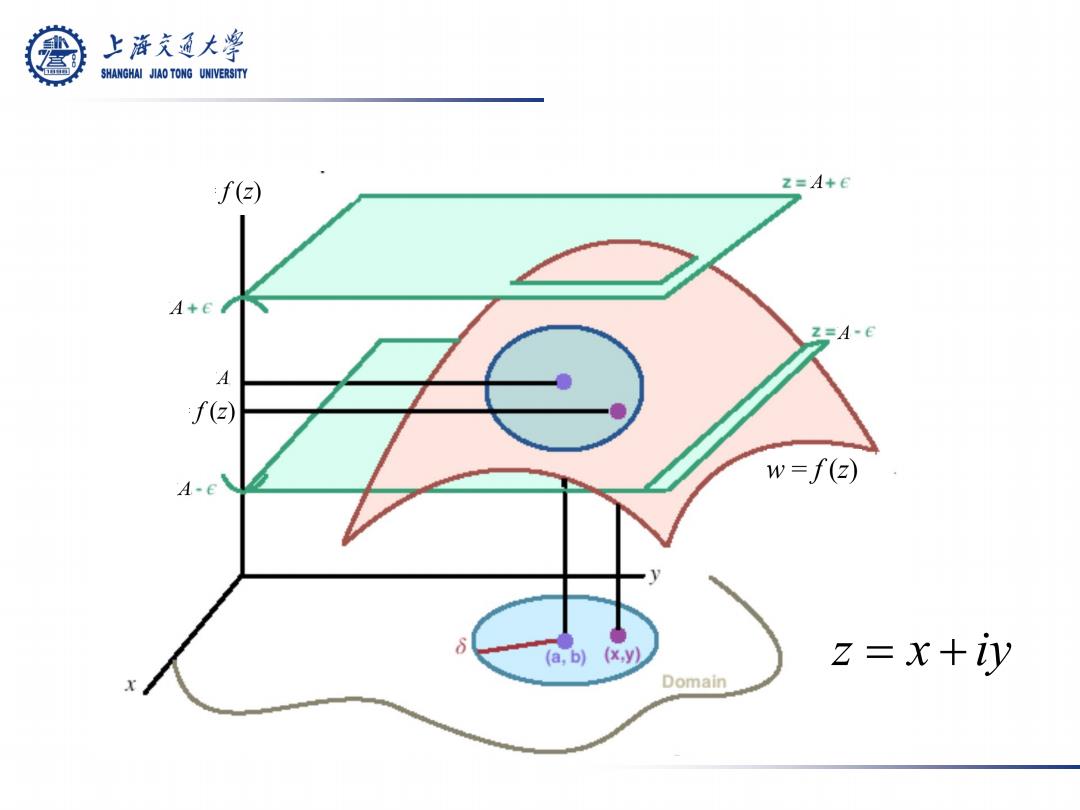
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY /(C) z=A+E A+E 2=A-E A f(z)) w=f(2) A-e (a,b)(x,y) Z= x iy Domain
z = x + iy

上游充通大 SHANGHAI JIAO TONG UNIVERSITY 复变函数极限的基本定理 设函数f(z)=u(x,y)+iv(x,y), 4=uo+ivo,zo=xo+ivo,limf(z)=A 的充要条件是 lim u(x,y)=uo lim v(x,y)vo x→x0,y>y0 x->x0,y->yo
0 , 0 , 0 0 0 0 0 lim ( , ) lim ( , ) , , lim ( ) ( ) ( , ) ( , ), 0 0 0 0 0 u x y u v x y v A u iv z x iy f z A f z u x y iv x y x x y y x x y y z z = = = + = + = = + → → → → → 的充要条件是 则 设函数 复变函数极限的基本定理