
法二先求直线上一定点:以z = 0代入383x-2y+0+1=0X72x+y-0-2=03.8于是得直线上的一定点1>因所求直线与两平面的法向量都垂直取s =n ×n, = (3,-2,1)×(2,1,-1) =(1,5,7)n83xⅡ3tz77对称式方程11517L
先求直线上一定点: 于是得直线上的一定点 取 s = n1 n2 = 对称式方程 5 7 7 8 1 7 3 z x y = − = − + − − = − + + = 2 2 0 3 2 1 0 x y z x y z , 7 3 x = ,0 , 7 8 , 7 3 因所求直线与两平面的法向量都垂直. (3,−2,1)(2,1,−1) = n2 n1 s 法二 以z = 0代入, 0 0 (1,5,7) 7 8 y = 1 2 L s
注意Z+3V+1x5783怎么不一样两个对称式方程15答:实际上直线的对称式方程不唯一。(当定点取得不同时对称式方程不同)38另外可验证,两个点(0,-1,-3),*都满足这两个对称式方程,过两点确定唯一的一条直线,因此这两个对称式方程表示同一条直线
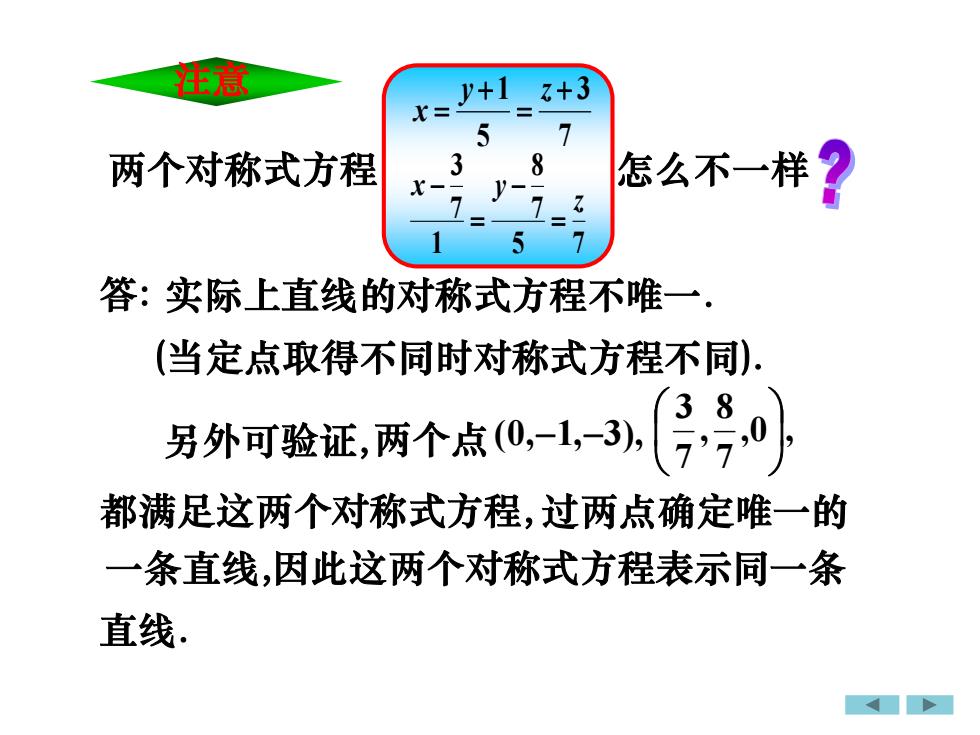
两个对称式方程 7 3 5 1 + = + = y z x 5 7 7 8 1 7 3 z x y = − = − 实际上直线的对称式方程不唯一. 注意 都满足这两个对称式方程, ,0 , 7 8 , 7 3 (0,−1,−3), 过两点确定唯一的 因此这两个对称式方程表示同一条 怎么不一样 答: (当定点取得不同时对称式方程不同). 另外可验证,两个点 一条直线, 直线