
x-xo_y-yo_z-mnD一般,如直线过两点M(Xi,J11),M,(X2,y2,Z2)则直线的一个向向量为:M,M, =(-网于是对称式方程可写成:x-Xi - - - z-ziX2 -Xi J2 -yiZ2 - Z1
( , , ), ( , , ) 1 1 1 1 2 2 2 2 M x y z M x y z 则直线的一个方向向量为: 于是对称式方程可写成: 2 1 1 2 1 1 2 1 1 z z z z y y y y x x x x − − = − − = − − p z z n y y m x x0 0 − 0 = − = − 一般, 如直线过两点 ( , , ) 2 1 2 1 2 1 = x − x y − y z − z M1M2

例2 一直线过点A(2,-3,4),且和y轴垂直相交Z求其方程解交点为勺 B(0,-3, 0)取 s= BAB0y= (2, 0, 4),Xx-2J+37. - 4所求直线方程204
解 交点为 B(0,−3, 0), 取 s = BA = (2, 0, 4), 所求直线方程 = − 2 x 2 . A . B s 例2 = + 0 y 3 . 4 z − 4 x y z O 一直线过点A(2,−3,4),且和y轴垂直相交, 求其方程
x-xo_y-yo_z-zo各类直线方程的互换mnD可将直线的对称式方程化为一般方程吗 注可将对称式方程拆为一般方程z-1x-1y-1如对称式方程为011x-1=0可写成一般方程(y-1=z-1 (即y-z =0)Zy-1z-1x-1又如001x=1可写成一般方程V=1L
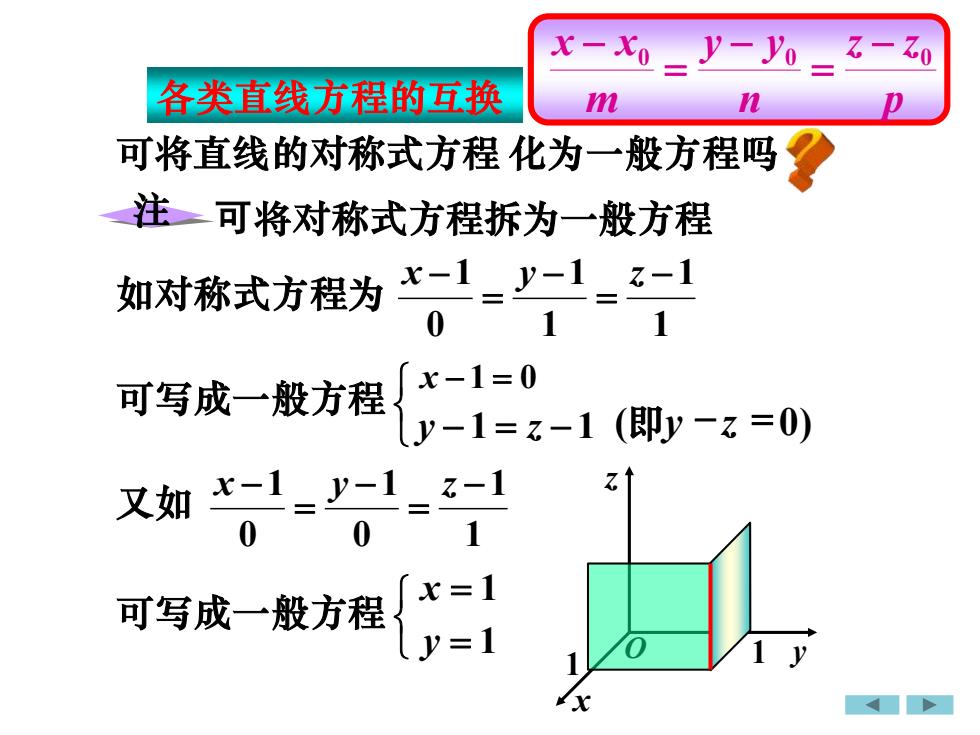
可将对称式方程拆为一般方程 如对称式方程为 1 1 1 1 0 1 − = − = x − y z 可写成一般方程 可将直线的对称式方程 又如 1 1 0 1 0 1 − = − = x − y z 注 可写成一般方程 p z z n y y m x x0 0 − 0 = − = − x − 1 = 0 y − 1 = z − 1 x = 1 y = 1 化为一般方程吗 各类直线方程的互换 x y z O 1 1 (即y −z = 0)

2.直线的一般方程化为对称式方程怎样将直线的一般方程化为对称式方程有两种方法(1)用代数的消元法化为比例式:2)在直线上找一定点,再求出方向向量即写出对称式方程
2. 直线的一般方程化为对称式方程 怎样将直线的一般方程 (1) 用代数的消元法化为比例式; 有两种方法 (2) 在直线上找一定点,再求出方向向量, 化为对称式方程 即写出对称式方程

3x-2y+z+1=0例3 将化为对称式方程2x+y-z-2=03x -20++1.= 0(1)解法一(2)2x +z2=0(1)+(2) =→ 5- y-1= 0-z-3=0(1) + 2(2)=7x两个方程中,每一个只有两个变量,解出共同的变量x.写成比例式即得对称式方程z+3y+1=57此直线上一定点为(0,-1,-3),方向向量为S =(1,5,7)
写成比例式 , 7 3 5 1 + = + = y z x 例3 解 法一 + − − = − + + = 2 2 0 3 2 1 0 x y z x y z (1) (2) 5x − y −1 = 0 (1) + 2(2) 7x − z − 3 = 0 (1) + (2) 两个方程中,每一个只有两个变量, 共同的变量 即得对称式方程. 解出 x. 此直线上一定点为(0,−1,−3),方向向量为s = (1,5,7) 将 化为对称式方程. + − − = − + + = 2 2 0 3 2 1 0 x y z x y z