
设有映射g:R→[-1,1],对每个xeR,g(x)=sinx例2映射f:[-1,1]→[0,1],对每个ue[-1,1],f(u)=1-求复合映射fg
例2 设有映射 对每个 映射 对每个 求复合映射
二、函数>定义设数集DCR.则称映射f:D→R为定义在D上的函数,通常简记为定义域y= f(x),xED+f(D)因变量自变量值域·注(1)注意符号f和f(α)的区别(2)表示函数的记号可以任意选取(3)函数的要素:定义域对应法则
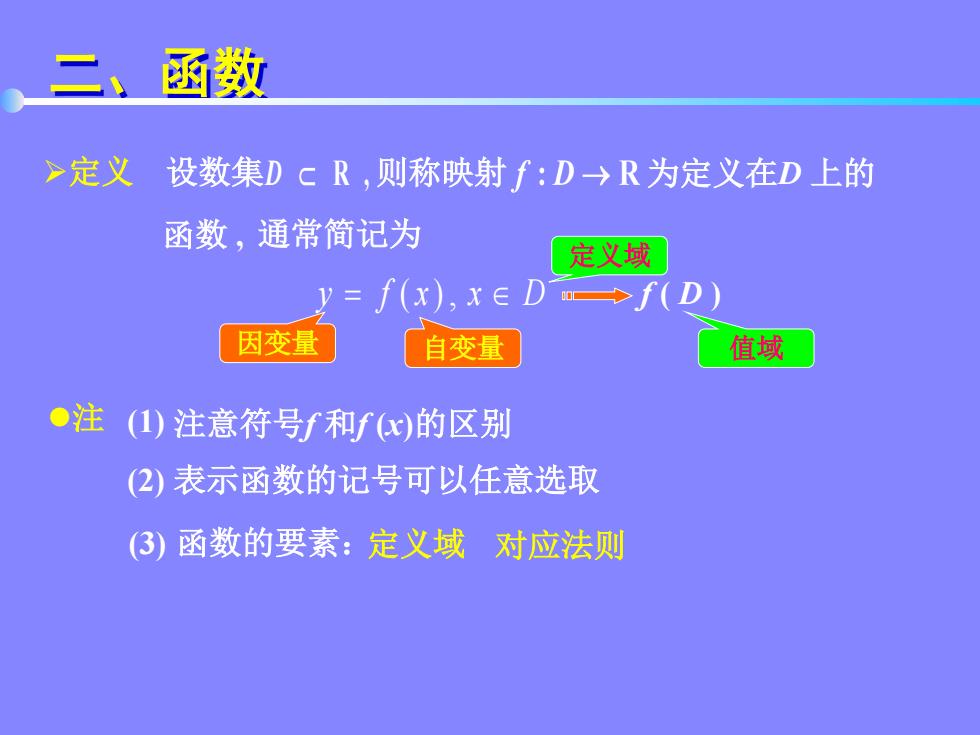
二、函数 定义 设数集 D R , 则称映射 为定义在D 上的 函数 , 通常简记为 y f ( x ) , x D f ( D ) 因变量 自变量 定义域 值域 注 (1) 注意符号f 和f (x)的区别 (2) 表示函数的记号可以任意选取 (3) 函数的要素:定义域 对应法则

函数的要素1.定义域自然定义域(1)定义域是非空的数集(2)定义域的求法:使表达式有意义的自变量的集合例3求函数f(x)=ln(4x-3)-arcsin(2x-1)的定义域2.对应法则(1)表示法:解析法表格法图象法(2)解析式的理解:一系列的运算程序1-4L-X例如: f(x)=理解为:f(△)1+△1+x
函数的要素 1.定义域 定义域是非空的数集 定义域的求法: (1) (2) 使表达式有意义的自变量的集合. 例3 求函数 f ( x ) l n ( 4 x 3 ) a r c s i n ( 2 x 1 ) 的定义域 2.对应法则 (1) 表示法:解析法 表格法 图象法 (2) 解析式的理解:一系列的运算程序 例如: x x f x 1 1 ( ) 理解为: 1 1 f ( ) 自然定义域