
X分布的性质 性质1(X分布的可加性) 设x~x2(n),3-x2(n2),并且x,独立, 则+好X2(+h) 此性质可以推广到多个随机变量的情形: 设x~x2(n),并且X(i=1,2,m)相互独立, 则2若+%+.+
2 分布的性质 性质1 2 2 2 2 2 2 1 1 2 2 1 2 2 2 2 1 2 1 2 ~ ( ), ~ ( ), , , ~ ( ). n n n n + + 设 并且 独立 则 2 ( ) 分布的可加性 此性质可以推广到多个随机变量的情形: 2 2 2 2 2 1 2 1 ~ ( ), ( 1, 2, , ) , ~ ( ). i i i m i m i n i m n n n = = + + + 设 并且 相互独立 则

43.N元=3 EX)=∫eidx=B.r受(aA>0zi 性质2(X分布的数学期望和方差) 若x2~X2(m),则E(x2)=n,D(x)=2n, 证明:x2=X+X+.+X,其中X,~N0,1), :E(X2)=D(X)+E2(X,)=1, x分布的定义式 D(X)=EX4)-[E(X=3-1=2,i=1,2,n. A4②x-2x的=n )x)2m
性质2 2 2 2 2 若 ~ ( ), n 则E n D n ( ) , ( ) 2 . = = 证明: ~ (0, 1), 其中X N i 2 2 ( ) ( ) ( ) E X D X E X i i i = + 2 4 2 2 ( ) ( ) [ ( )] D X E X E X i i i = − i n = 1, 2, , . 2 2 1 ( ) n i i E E X = = 2 1 ( ) n i i E X = = = n, 2 2 1 ( ) n i i D D X = = 2 1 ( ) n i i D X = = = 2 . n 2 ( ) 分布的数学期望和方差 = − = 3 1 2, 2 2 2 2 = + + + X X X 1 2 n, 2 = 1, 分布的定义式 2 5 4 4 2 2 0 2 2 1 5 4 3 1 ( ) d 2 ( ) 3 2 2 2 2 2 2 x E X x e x i + − = = = = 2 1 2 0 1 d ( ) ( , 0) 2 2 x x e x + − − =

2.t分布 设X~N(0,1),Y~x(n),且X,Y独立,则称随机变量 X t-Yin 服从自由度为n的t分布,记为t~t(n) t分布又称学生氏(Student)分布, t(n)分布的概率密度函数为 h(t)= -0<t<+0
2 ~ (0, 1), ~ ( ~ ( ). ) , , / X N Y n X t t t n Y X t n Y n = 设 ,且 独立,则称随机变量 服从自由度为 的 分布 记为 t 分布又称学生氏(Student)分布. 1 2 2 1 2 ( ) 1 , π 2 n n t h t t n n n + − + = + − + t n( )分布的概率密度函数为 2. t 分布
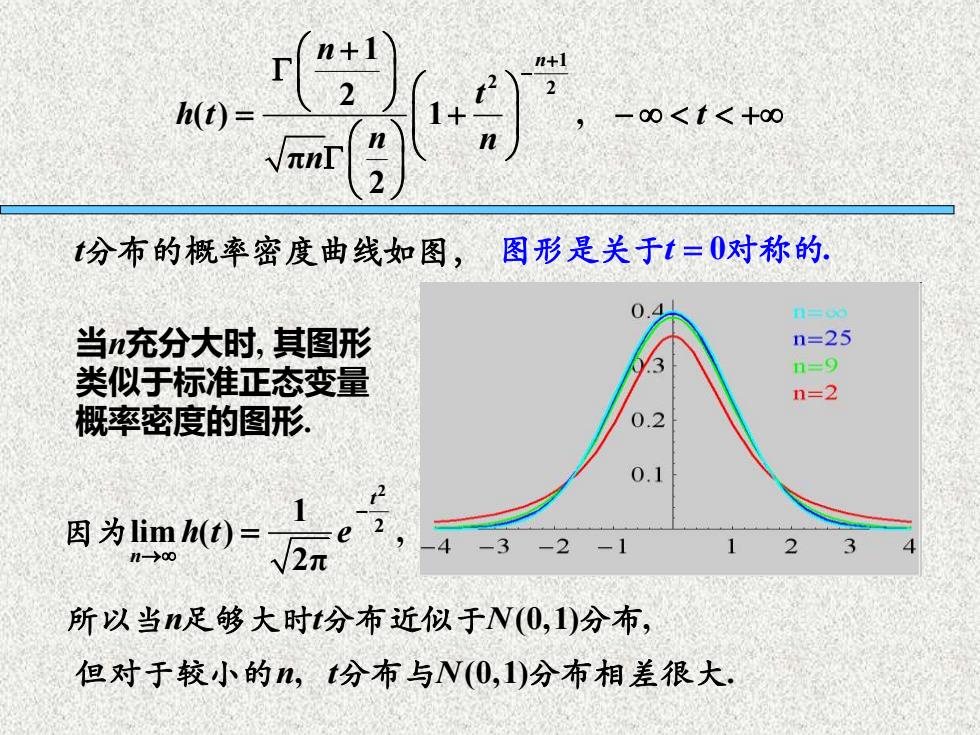
h()= -0<t<+00 t分布的概率密度曲线如图,图形是关于t=0对称的. 0.4 当n充分大时,其图形 n=25 3 类似以于标准正态变量 n=9 n=2 概率密度的图形. 0.2 0.1 因为limh(t)= 1 1-→o0 √2元 -3-2 一1 2 3 所以当n足够大时t分布近似于N(0,1)分布, 但对于较小的n,t分布与N(0,1)分布相差很大
t分布的概率密度曲线如图, 图形是关于t = 0 . 对称的 当n充分大时, 其图形 类似于标准正态变量 概率密度的图形. 2 2 1 lim ( ) , 2π t n h t e − → 因为 = 所以当n t N 足够大时 分布近似于 (0,1) , 分布 但对于较小的n t N , (0,1) . 分布与 分布相差很大 1 2 2 1 2 ( ) 1 , π 2 n n t h t t n n n + − + = + − +