
一般地, 设x1,x2,xn是总体F的一个容量为n的样本值, 将x1,x2,x按自小到大的顺序重新排列,并重新编 号,记为x山≤x2)≤.≤xm2 则经验分布函数的观察值为 0 x<X四 . F(x)= k xO≤x<xk+l n 1 xm≤x
一般地, 设 x x xn , , , 1 2 是总体F的一个容量为n的样本值, 将x x xn , , , 1 2 按自小到大的顺序重新排列,并重新编 号,记为 x(1) x(2) x(n), (1) ( ) ( 1) ( ) 0 ( ) . 1 n k k n x x k F x x x x n x x + = 则经验分布函数的观察值为

格里汶科定理对于任一实数x,当n→o时, Fn(x)以概率1收敛于分布函数F(x),即 P-即-fw=-l 说明:对于任一实数x,当n充分大时,经验 分布函数的任一观察值F(x)与总体分布函数 F(x)只有微小的差别,从而可当作F(x)来使用
格里汶科定理 对于任一实数 x,当n → 时, F ( x) n 以概率 1 收敛于分布函数F(x),即 lim sup ( ) ( ) 0 = 1 − = − + → P F x F x n x n 。 说明:对于任一实数 x,当 n 充分大时,经验 分布函数的任一观察值 F (x) n 与总体分布函数 F(x) 只有微小的差别,从而可当作 F(x) 来使用
三、统计三大抽样分布 统计量的分布称为抽样分布 要求:牢记三大分布的定义、性质、密度函数图形轮廓; 并能够查表计算. (一)X分布设X,X2,·,Xn是来自总体N0,)的一个样本, 则称统计量x=X?+X好+.+X服从自由度为n的x分布,记 为x~x(m)。自由度指定义式中包含的独立变量的个数. f(y)1 概率密度为 n=4 -y2e2,y>0 f)=22r 0 其它 随着的增大,密度曲线逐渐趋于平缓、对称
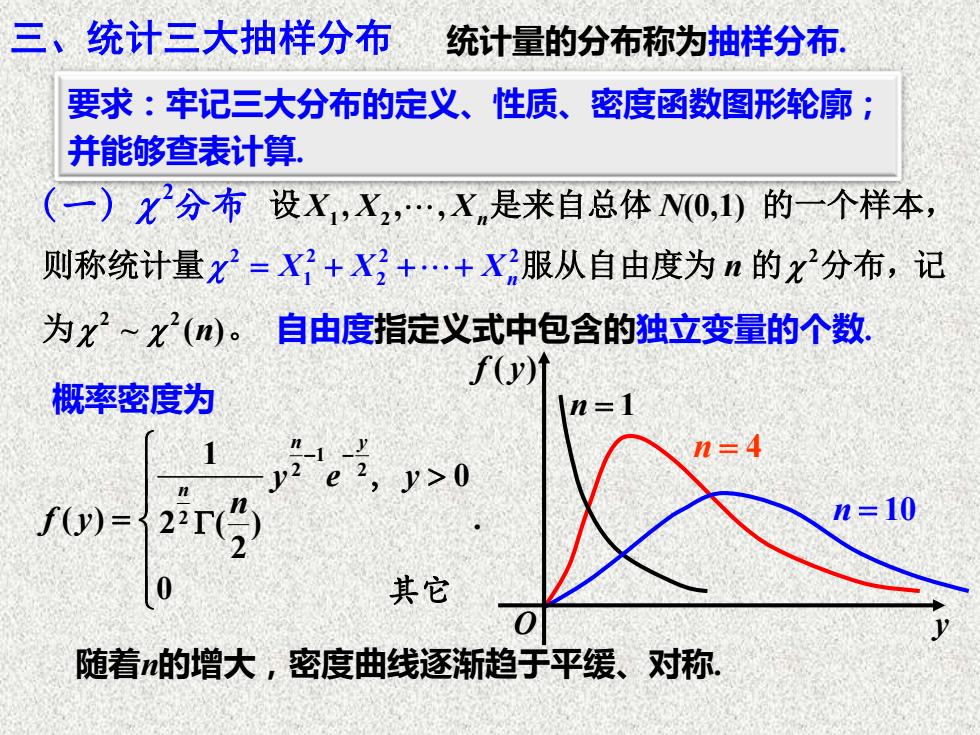
三、统计三大抽样分布 统计量的分布称为抽样分布. 2 (一) 分布 设 1 2 , , , X X Xn是来自总体 N(0,1) 的一个样本, 则称统计量 2 2 2 2 = + + + X X X 1 2 n服从自由度为 n 的 2 分布,记 为 2 2 ~ ( ) n 。 自由度指定义式中包含的独立变量的个数. 1 2 2 2 1 0 ( ) . 2 ( ) 2 0 n y n y e y n f y − − = , 其它 概率密度为 n = 4 n = 10 n = 1 随着n的增大,密度曲线逐渐趋于平缓、对称. 要求:牢记三大分布的定义、性质、密度函数图形轮廓; 并能够查表计算. y f y( )O

P51第二章第5节例3 XN0,0→y=X2-20=r52) P78第三章第5节例3 X;~T(a,)(i=1,2,.,n)且相互独立 x+x,+.x-(o0)
P51 第二章第5节例3 P78 第三章第5节例3 X N~ (0, 1) 2 2 = Y X ~ (1) 1 ( 2) 2 = , ~ ( , )( 1,2, , ) X i n i i = 且相互独立 1 2 1 ~ ( , ) n n i i X X X = + + +

下面推导x(n)的概率密度: 现X,~N(0,1),由定义X~x(I), 即X-r22.=12,m. 再由X1,X2,Xn相互独立知X,X,X 也相互独立, 由Γ分布的可加性知父-2x:-r《22 即得x()分布的概率密度,如前面所示
再由X X Xn , , , 1 2 相互独立知 由分布的可加性知 即得 ( ) 2 n 分布的概率密度,如前面所示。 2 2 2 2 1 , , , X X Xn 也相互独立, 下面推导 ( ) 2 n 的概率密度: 即 2) 2 1 ~ ( 2 Xi , ,(i = 1, 2, , n)。 现X ~ N(0, 1) i , 由定义 ~ (1) 2 2 Xi , 2 2 1 n i i X = = ~ ,2 , 2 n