4.复数的三角表示和复数的方根 z=x+iy 复平面C的不为零的点z=x+1y 极坐标(r,O):x=rcos0,y=rsin8 r=el, 是正实轴与从原点O到z的射线的 图1.3模、幅角 夹角,称为复数z的幅角,记为0=Argz 满足条件-π<O≤π的幅角称为Agz的主值,记为 0arg,于是有0Arg=argz+2k饥,k-0,±1,±2,. 复数的三角表示=r(cos0升isin0 复数的指数形式 z=reio
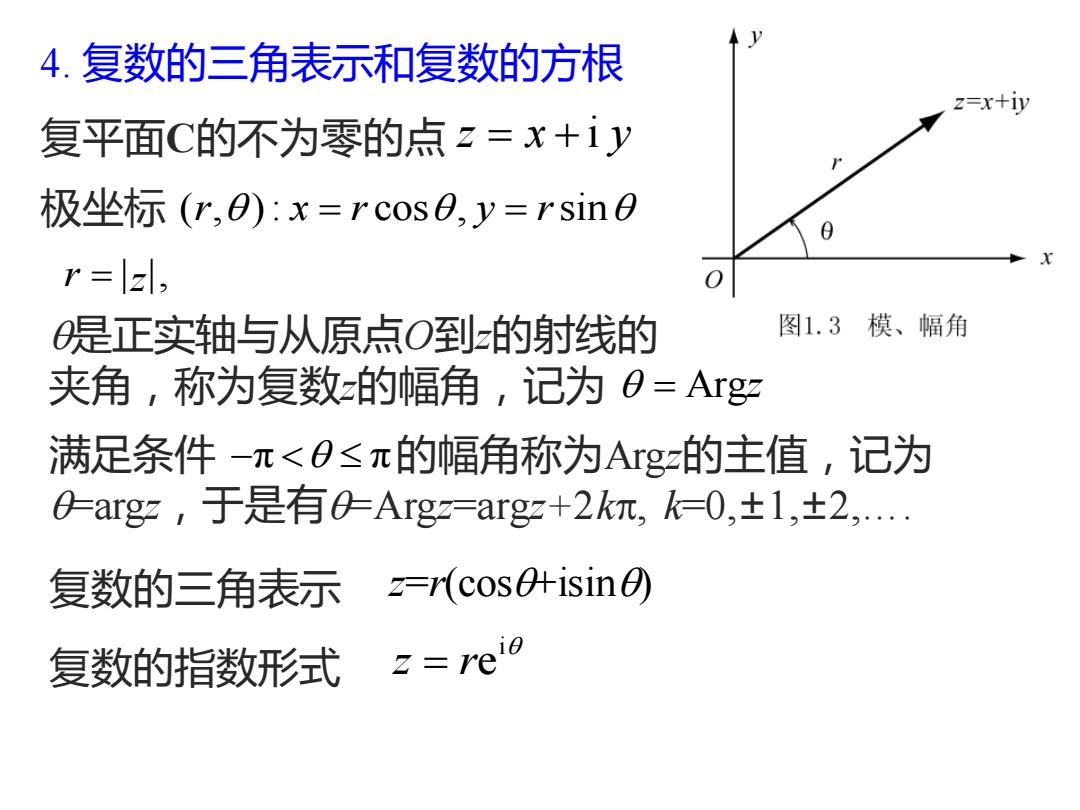
4. 复数的三角表示和复数的方根 复平面C的不为零的点 z x y = + i 极坐标 ( , ) : cos , sin r x r y r = = r = z , 是正实轴与从原点O到z的射线的 夹角,称为复数z的幅角,记为 = Argz 满足条件 的幅角称为Argz的主值,记为 =argz,于是有=Argz=argz+2k, k=0,±1,±2,…. − π π 复数的三角表示 z=r(cos+isin) 复数的指数形式 i z re =

例1.1求Arg(-3-i4) 解:Arg(-3-i4)Farg(-3-i4)+2km,k=0,±1,±2,. 点-3-4位于第三象限 (-4) 4 arg(-3-i4)=arctan 元=arctan--π (-3) 3 4 Arg(-3-i4)=arctan。+(2k-l)π, =0,±1,±2,. 例1.2计算z=em 解:eπ=cosπ+isinπ=-l
例1.1 求Arg(-3-i4). 解: Arg(-3-i4)= arg(-3-i4)+2k, k=0,±1,±2,…. 点-3-i4位于第三象限 ( 4) 4 arg( 3 i 4) arctan π arctan π ( 3) 3 − − − = − = − − 4 Arg( 3 i 4) arctan (2 1)π, 3 − − = + −k k=0,±1,±2,…. 例1.2 计算 i π z = e i π 解: e cos = + = − π isin π 1