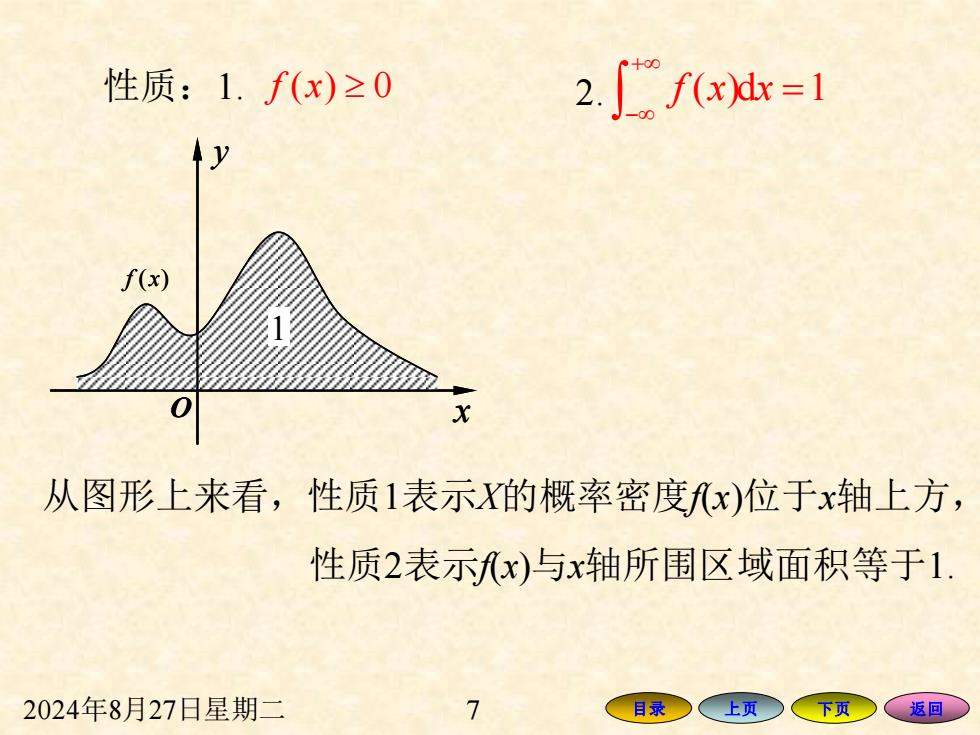
性质:1.f(x)≥0 2.∫f(x=1 f(x 从图形上来看,性质1表示X的概率密度fx)位于x轴上方, 性质2表示x)与x轴所围区域面积等于1 2024年8月27日星期二 7 目录 上页 下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 性质:1. f x( ) 0 2. ( )d 1 + − = f x x O x y 1 f x( ) 1 O x y 1 f x( ) 1 从图形上来看,性质1表示X的概率密度f(x)位于x轴上方, 性质2表示f(x)与x轴所围区域面积等于1
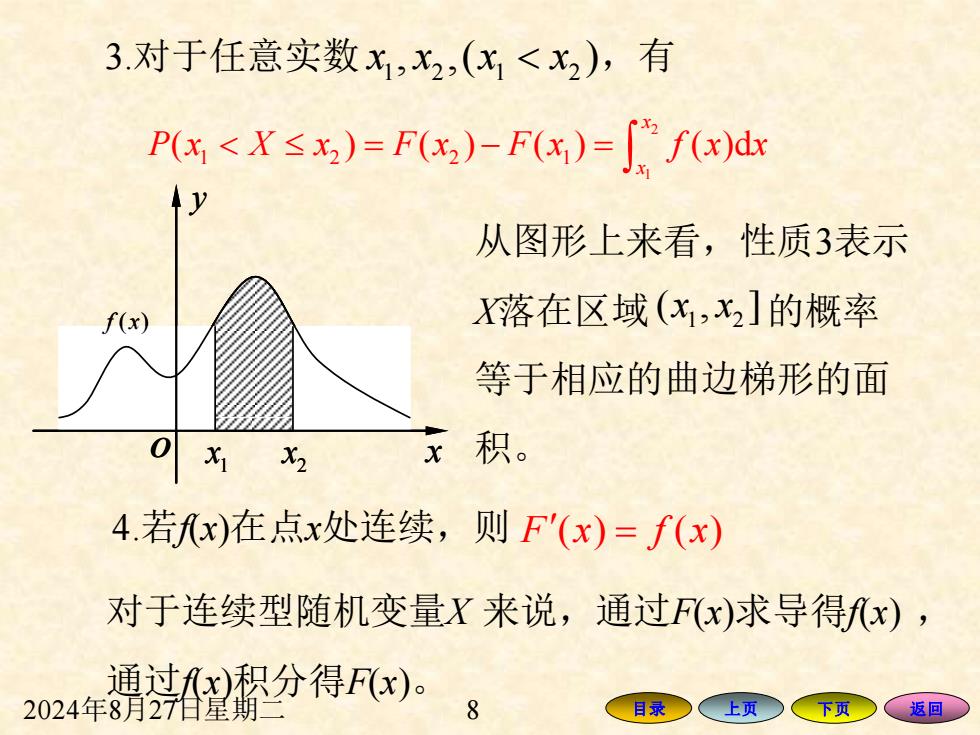
3.对于任意实数x,x2,(x<x2),有 Px<X≤x)=F(x)F(x)=∫fx)d 从图形上来看,性质3表示 f(x) 落在区域(x,x2]的概率 等于相应的曲边梯形的面 x积。 4.若x)在点x处连续,则F'(x)=f(x) 对于连续型随机变量X来说,通过Fx)求导得x), 通过x积分得F(x)。 2024年8月27日星期 目录 上页 下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 3.对于任意实数 x x x x 1 2 1 2 , ,( ) ,有 2 1 1 2 2 1 ( ) ( ) ( ) ( )d = − = x x P x X x F x F x f x x O x y 1 f x( ) 1 x 2 O x x y 1 f x( ) 1 x 2 x 从图形上来看,性质3表示 X落在区域 的概率 等于相应的曲边梯形的面 积。 1 2 ( , ] x x 4.若f(x)在点x处连续,则 F x f x ( ) ( ) = 对于连续型随机变量X 来说,通过F(x)求导得f(x) , 通过f(x)积分得F(x)

5.连续型随机变量取任一指定实数值的概率为零. 即 P{X=x}=0 由性质5,易得: P(x<X≤x2)=P(x≤X≤x2)=P(x1<X<x2) =Px≤X<x)=∫fx)dr 注:对离散型随机变量,上式不成立。 2024年8月27日星期二 目录 、上页 下页 、返回
2024年8月27日星期二 9 目录 上页 下页 返回 5.连续型随机变量取任一指定实数值的概率为零. 即 P X x = = 0 0 由性质5,易得: 1 2 1 2 1 2 P x X x P x X x P x X x ( ) ( ) ( ) = = 2 1 1 2 = = ( ) ( )d x x P x X x f x x 注:对离散型随机变量,上式不成立

几种常见的连续型随机变量的分布 均匀分布 定义:若连续型随机变量X的概率密度为 1 f(x)= b-a a≤x≤b, 0, 其它 则称x服从[a,b]上的均匀分布。记为X~U[a,b] 意义:X“等可能”地取区间,中的值,这里的“等可 能”理解为:X落在间 中任意等长度的子区间内的可能 性是相同的。即等长度,等概率。 2024年8月27日星期二 10 目录○ 上页> 下页 返回
2024年8月27日星期二 10 目录 上页 下页 返回 几种常见的连续型随机变量的分布 均匀分布 定义:若连续型随机变量X的概率密度为 1 , , ( ) 0, a x b f x b a = − 其它. 则称X服从 a b, 上的均匀分布。记为 X U a b , 意义:X“等可能”地取区间 中的值,这里的“等可 能”理解为:X落在区间 中任意等长度的子区间内的可能 性是相同的。即等长度,等概率。 a b, a b,

正态分布 定义:若连续型随机变量X的概率密度为 1 (x-)2 f(x)= e 2o2 ,-00<X<十0, √2元·0 其中u,o(o>0)为常数,则称X服从参数为u和o2的正态分布 记为X~W(4,o) 正态分布的分布函数: 2024年8月27日星期二 11 目录○ 、上页 下页 返回
2024年8月27日星期二 11 目录 上页 下页 返回 正态分布 定义:若连续型随机变量X的概率密度为 2 2 ( ) 2 1 ( ) e , , 2 x f x x − − = − + 其中μ, 为常数,则称X服从参数为μ和 的正态分布 2 ( 0) 2 记为 2 X N( , ) 正态分布的分布函数: 2 2 ( ) 2 1 ( ) e d 2π t x F x t − − − =