
若D不满足以上条件则可通过加辅助线将其分割2为有限个上述形式的区域,如图IDHLDnXHIGH EDUCATION PRESS定理1目录返回上页下页结束
y o x L 2) 若D不满足以上条件, 则可通过加辅助线将其分割 D1 Dn D2 为有限个上述形式的区域 , 如图 定理1 目录 上页 下页 返回 结束
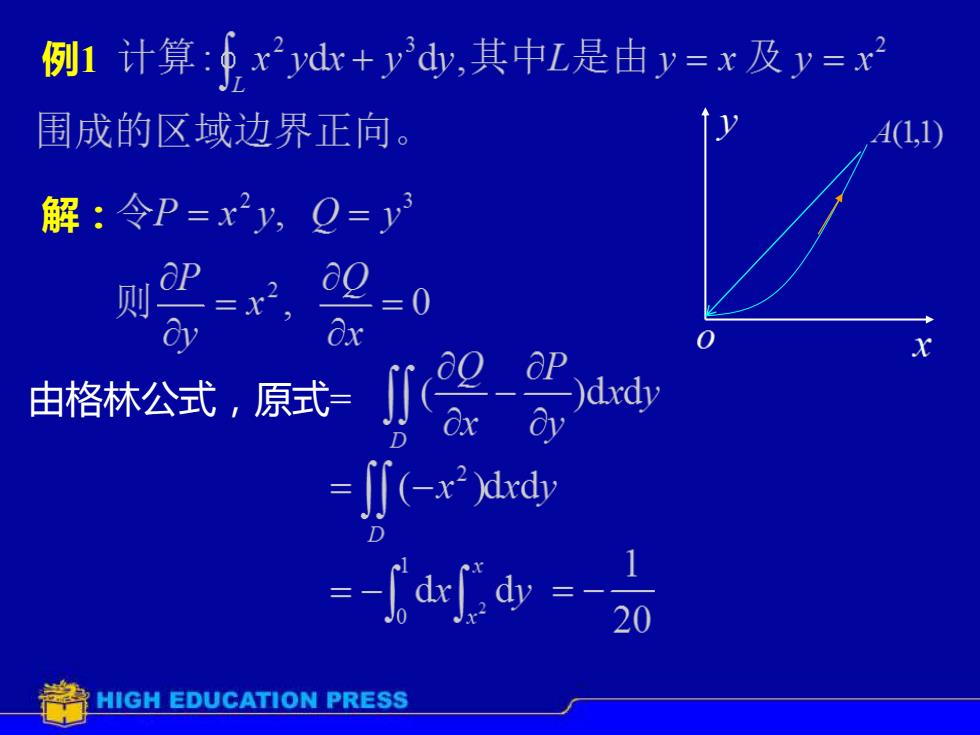
例1计算:xydx+dy,其中L是由=x及=x围成的区域边界正向A(1,1)解:令P=xy,Q=yapaQ则CoydXxapag1)dxdy由格林公式,原式axOyD= Jf(-x)dxdy20HIGH EDUCATION PRESS
例1 解: 由格林公式,原式=

edxdy,其中D 是以 O(0,0),A(1,1),例2. 计算DB(0,1)为顶点的三角形闭域Q= xe-y2,则解: 令P=0,A(1,1)apB(0,1)OxdyDy=x利用格林公式,有xdxdyxedyxeAHIGH EDUCATION PRESS返回结束机动目录上页下页
例2. 计算 ,其中D 是以 O(0,0) , A(1,1) , B(0,1) 为顶点的三角形闭域 . 解: 令 , 则 2 0, y P Q xe − = = 利用格林公式 , 有 x e y OA y d 2 − = ye y y d 1 0 2 − = (1 ) 2 1 −1 = − e y = x o y x A(1,1) B(0,1) D 机动 目录 上页 下页 返回 结束

-0%oQdxdy=dPdx+Qdy格林公式的应用:ax1.利用二重积分计算曲线积分(注意条件)(1)L为闭曲线正向:aPag(2)在D上连续。ax2.求平面区域的面积正向闭曲线L所围区域D的面积xdy-ydxHIGH EDUCATION PRESS
格林公式的应用: 1. 利用二重积分计算曲线积分(注意条件) 2. 求平面区域的面积