
第十二章习题课求和与展开级数的收敏、数项级数的审敛法一、二、求幂级数收敛域的方法三、幂级数和函数的求法四、函数的幂级数和傅里叶级数展开法
习题课 级数的收敛、求和与展开 三、幂级数和函数的求法 四、函数的幂级数和傅里叶级数 展开法 一、数项级数的审敛法 二、求幂级数收敛域的方法 第十二章

8求和ZtS(x)(在收敛域内进行)un(x)A展开n=0当x=xo 时为数项级数;8Z当un(x)=anx时为幂级数;un(x)n=0当un(x) = an cos nx + bn sinnx(αn,bn 为傅里叶系数)时,为傅里叶级数基本问题:判别敛散;求收敛域;求和函数;级数展开
求和 展开 (在收敛域内进行) 基本问题:判别敛散; 求收敛域; 求和函数; 级数展开. 为傅里叶系数) 时, 为傅里叶级数. 时为数项级数; 时为幂级数; an bn (

数项级数的审敛法一、1.利用部分和数列的极限判别级数的敛散性Cun收敛台(s收敛>n=1lim un = On→8
一、数项级数的审敛法 1. 利用部分和数列的极限判别级数的敛散性
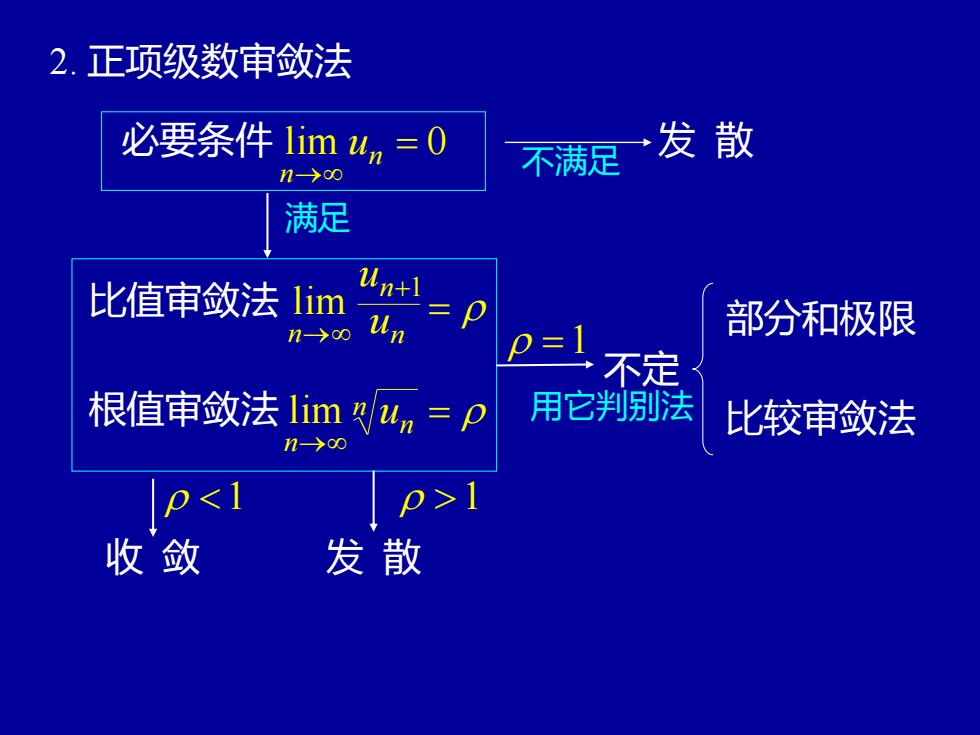
2.正项级数审敛法→发散必要条件lim un, = 0不满足n→0满足Un+l比值审敛法lim部分和极限Un-→00p=l不定用它判别法根值审敛法limn/un =p比较审敛法n>8p<1p>1收敛发散
2. 正项级数审敛法 必要条件 lim = 0 → n n u 不满足 发 散 满足 比值审敛法 lim n→ un+1 un = 根值审敛法 = → n n n lim u 1 收 敛 发 散 =1 不定 用它判别法 比较审敛法 部分和极限 1

3.任意项级数审敛法82un为收敛级数概念:n=188ZZ若收敛,称u绝对收敛unnn=1n=l808Z若发散,称条件收敛u>nn=1n=l若un≥un+1>0,且 lim un =0Leibniz判别法:n008≤un+l:收敛,且余项Z(-1)"un 则交错级数nn=l
3. 任意项级数审敛法 为收敛级数 Leibniz判别法: 若 且 则交错级数 收敛 , 概念: 且余项 若 收敛 , 称 绝对收敛 若 发散 , 称 条件收敛